题目内容
设函数 若关于x的方程f2(x)=af(x)恰有四个不同的实数解,则实数a的取值范围为( )
若关于x的方程f2(x)=af(x)恰有四个不同的实数解,则实数a的取值范围为( )A.(-∞,0)
B.(0,1)
C.[0,1]
D.(1,+∞)
【答案】分析:由已知中函数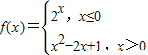 若关于x的方程f2(x)=af(x)恰有四个不同的实数解,我们可以根据函数f(x)的图象得到f(x)=a恰有三个不同的实数解,进而得到实数a的取值范围.
若关于x的方程f2(x)=af(x)恰有四个不同的实数解,我们可以根据函数f(x)的图象得到f(x)=a恰有三个不同的实数解,进而得到实数a的取值范围.
解答:解:函数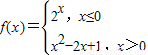 的图象如下图所示:
的图象如下图所示:

关于x的方程f2(x)=af(x)可转化为:
f(x)=0,或f(x)=a,
若关于x的方程f2(x)=af(x)恰有四个不同的实数解,
则f(x)=a恰有三个不同的实数解,
由图可知:0<a<1
故选B
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据已知中函数的解析式,画出函数的图象,再利用数形结合是解答本题的关键.
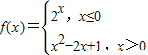 若关于x的方程f2(x)=af(x)恰有四个不同的实数解,我们可以根据函数f(x)的图象得到f(x)=a恰有三个不同的实数解,进而得到实数a的取值范围.
若关于x的方程f2(x)=af(x)恰有四个不同的实数解,我们可以根据函数f(x)的图象得到f(x)=a恰有三个不同的实数解,进而得到实数a的取值范围.解答:解:函数
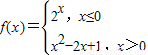 的图象如下图所示:
的图象如下图所示:
关于x的方程f2(x)=af(x)可转化为:
f(x)=0,或f(x)=a,
若关于x的方程f2(x)=af(x)恰有四个不同的实数解,
则f(x)=a恰有三个不同的实数解,
由图可知:0<a<1
故选B
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据已知中函数的解析式,画出函数的图象,再利用数形结合是解答本题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
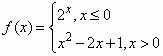 若关于x的方程f2(x)=af(x)恰有四个不同的实数解,则实数a的取值范围为
若关于x的方程f2(x)=af(x)恰有四个不同的实数解,则实数a的取值范围为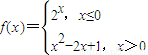 若关于x的方程f2(x)=af(x)恰有四个不同的实数解,则实数a的取值范围为( )
若关于x的方程f2(x)=af(x)恰有四个不同的实数解,则实数a的取值范围为( )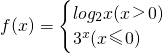 若关于x的方程f(x)=a有两个不相等的实数根,则实数a的取值范围是________.
若关于x的方程f(x)=a有两个不相等的实数根,则实数a的取值范围是________.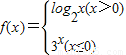 若关于x的方程f(x)=a有两个不相等的实数根,则实数a的取值范围是 .
若关于x的方程f(x)=a有两个不相等的实数根,则实数a的取值范围是 .