题目内容
已知等差数列的前13的和为39,则a6+a7+a8=( )
分析:由求和公式和性质可得a7的值,而所求等于3a7,代入计算可得.
解答:解:由题意可得等差数列的前13的和
S13=
=
=39
解之可得a7=3,又a6+a8=2a7
故a6+a7+a8=3a7=9
故选D
S13=
| 13(a1+a13) |
| 2 |
| 13×2a7 |
| 2 |
解之可得a7=3,又a6+a8=2a7
故a6+a7+a8=3a7=9
故选D
点评:本题考查等差数列的性质和求和公式,划归为a7是解决问题的关键,属基础题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
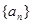 的前13项之和为
的前13项之和为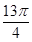 ,则
,则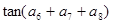 等于
等于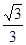 B.
B. 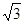 C.
C. 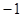 D.
D. 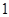
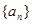 的前13项之和为
的前13项之和为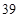 ,则
,则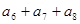 等于(
)
等于(
)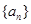 的前13项之和为
的前13项之和为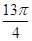 ,则
,则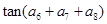 等于 ( )
等于 ( ) B.
B.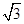 C.—1 D.1
C.—1 D.1 的前13项之和为
的前13项之和为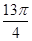 ,则
,则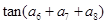 等于( )
等于( ) 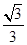 B.
B.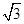 C.—1 D.1
C.—1 D.1