题目内容
已知奇函数f(x)满足f(x+1)=f(x-l),给出以下命题:①函数f(x)是周期为2的周期函数;②函数f(x)的图象关于直线x=1对称;③函数f(x)的图象关于点(k,0)(k∈Z)对称;④若函数f(x)是(0,1)上的增函数,则f(x)是(3,5)上的增函数,其中正确命题的番号是( )
| A.①③ | B.②③ | C.①③④ | D.①②④ |
A
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
我们把具有以下性质的函数 称为“好函数”:对于在
称为“好函数”:对于在 定义域内的任意三个数
定义域内的任意三个数 ,若这三个数能作为三角形的三边长,则
,若这三个数能作为三角形的三边长,则 也能作为三角形的三边长.现有如下一些函数:
也能作为三角形的三边长.现有如下一些函数:
① ②
②
③ ,
, ④
④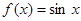 ,
, .
.
其中是“好函数”的序号有( )
| A.①② | B.①②③ | C.②③④ | D.①③④ |
若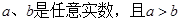 ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )
A. | B. |
C.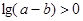 | D.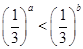 |
设函数 是定义在R上以
是定义在R上以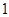 为周期的函数,若
为周期的函数,若 在区间
在区间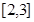 上的值域为
上的值域为 ,则函数
,则函数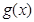 在
在 上的值域为 ( )
上的值域为 ( )
A. | B. | C.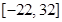 | D. |
下列函数中,既是奇函数,又在(0,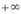 )上单调递减的函数是 ( )
)上单调递减的函数是 ( )
A.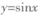 | B.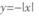 | C.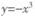 | D.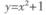 |
若函数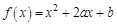 有两个不同的零点,则
有两个不同的零点,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D.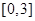 |
函数y= 的值域是
的值域是
A.[ 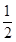 ,+ ,+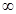 ) ) | B.[ ,1) ,1) | C.(0,1) | D.[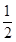 ,1〕 ,1〕 |
已知 ,则
,则 ]的值为 ( )
]的值为 ( )
| A.-2 | B.2 | C.-3 | D.3 |
已知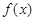 在
在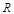 上是奇函数,且满足
上是奇函数,且满足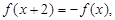 当
当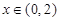 时,
时,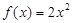 ,则
,则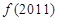 等于 ( )
等于 ( )
A.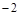 | B.2 | C.-98 | D.98 |