题目内容
若关于x的方程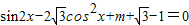
在区间
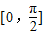上有两个不同的解，则实数m的取值范围是（ ）A．
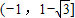
B．
C．
D．
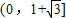
【答案】分析：这种题目首先要分离参数，把m表示出来，整理关于三角函数的解析式，根据余弦曲线的特点看出若有两个交点时，m应该在的区间．
解答：解：∵关于x的方程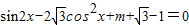
在区间
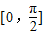上有两个不同的解，
∴m=2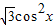
-sin2x+1-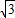
=
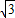cos2x-sin2x+1
=2cos（2x+
）+1
∵在区间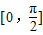
上有两个不同的解，
只要写出函数的值域，当x∈
时，
2x+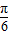
∈[
]
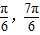根据余弦函数的图象可以知道函数在这个区间上，若是直线y=m与曲线有两个交点，
则m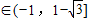
，
故选A．
点评：本题考查函数的定义域和值域，本题解题的关键是分离参数，把m看成是函数，求函数的值域即可．
解答：解：∵关于x的方程
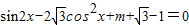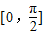在区间上有两个不同的解，∴m=2
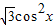-sin2x+1-=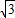
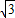cos2x-sin2x+1=2cos（2x+
）+1∵在区间
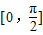上有两个不同的解，只要写出函数的值域，当x∈
时，2x+
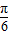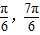∈[]根据余弦函数的图象可以知道函数在这个区间上，若是直线y=m与曲线有两个交点，
则m
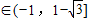，故选A．
点评：本题考查函数的定义域和值域，本题解题的关键是分离参数，把m看成是函数，求函数的值域即可．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数f（x）=-4cos2x+4cosx+1-a，若关于x的方程在区间[-
，
]上有解，则a的取值范围是（ ）
| π |
| 4 |
| 2π |
| 3 |
| A、[-8，0] | ||
| B、[-3，5] | ||
| C、[-4，5] | ||
D、[-3，2
|
在 
处取得极值0.
在区间
上恰有两个相异实数根，求实数m的
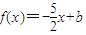在区间[0，2]上恰有两个不同的实数根，求实数b的取值范围；
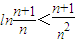都成立．
在区间[0，2]上恰有两个不同的实数根，求实数b的取值范围；
都成立．
．
时，不等式
恒成立，求实数m的取值范围；
在区间[1，3]上恰好有两个相异的实根，求实数
的取值范围．