题目内容
将杨辉三角中的奇数换成1，偶数换成0，得到0-1三角数表，从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，第5次全行的数都为1的是第（ ）行．分析：先由条件找到全行的数都为1的前几项，利用前几项的规律来求出全行的数都为1的行的通项即可．
解答：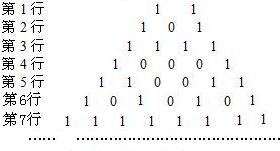
解：由题意得，全行的数都为1的分别是：
第1行，第3行，第7行，…
又因为数1，3，7，…的通项为2n-1
所以第n次全行的数都为1的是第2n-1行，
当n=5时，第5次全行的数都为1的是第25-1=31行
故选A．
解：由题意得，全行的数都为1的分别是：第1行，第3行，第7行，…
又因为数1，3，7，…的通项为2n-1
所以第n次全行的数都为1的是第2n-1行，
当n=5时，第5次全行的数都为1的是第25-1=31行
故选A．
点评：本题是借助于杨辉三角求数列的通项公式，本题的关键点是熟悉杨辉三角以及常见数列的通项公式．
练习册系列答案
相关题目
将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的0-1三角数表．从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，设第n次全行的数都为1的是第x行；第61行中1的个数是y，则x、y的值分别是（ ）