题目内容
现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙、丙不会开车但能从事其他三项工作,丁、戊都能胜四项工作,则不同安排方案的种数是( )
| A.240 | B.126 | C.78 | D.72 |
C
解析试题分析:根据题意,分情况讨论,①甲、乙、丙三人中有两人在一起参加除了开车的三项工作之一,有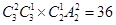 种;②甲、乙、丙三人各自1人参加除了开车的三项工作之一即丁、戌两人一起参加开车工作时,有
种;②甲、乙、丙三人各自1人参加除了开车的三项工作之一即丁、戌两人一起参加开车工作时,有 种;③甲、乙、丙三人中有一1人与丁、戌中的一人一起参加除开车的三项工作之一,有
种;③甲、乙、丙三人中有一1人与丁、戌中的一人一起参加除开车的三项工作之一,有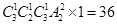 种,由分类计数原理,可得共有
种,由分类计数原理,可得共有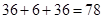 种,故选C.
种,故选C.
考点:1.两个计数原理;2.排列组合的综合问题.

练习册系列答案
相关题目
设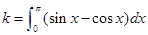 ,若
,若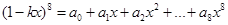 ,
,
则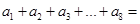 ( )
( )
| A.-1 | B.0 | C.l | D.256 |
设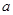 ,
,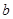 ,
,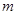 为整数(m>0),若
为整数(m>0),若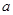 和
和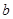 被
被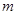 除得的余数相同,则称
除得的余数相同,则称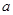 和
和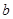 对模
对模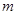 同余,记为
同余,记为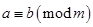 .若
.若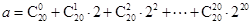 ,
,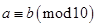 ,则
,则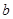 的值可以是( )
的值可以是( )
| A.2011 | B.2012 | C.2013 | D.2014 |
二项式 的展开式中
的展开式中 的系数是( )
的系数是( )
| A.84 | B.-84 | C.126 | D.-126 |
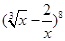 二项展开式中的常数项为( )
二项展开式中的常数项为( )
| A.56 | B.-56 | C.112 | D.-112 |
对于二项式 ,四位同学作出了四种判断:
,四位同学作出了四种判断:
①存在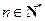 ,展开式中有常数项
,展开式中有常数项
②对任意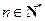 ,展开式中没有常数项
,展开式中没有常数项
③对任意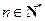 ,展开式中没有x的一次项
,展开式中没有x的一次项
④存在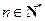 ,展开式中有x的一次项.
,展开式中有x的一次项.
上述判断中正确的是( )
| A.①③ | B.②③ | C.②④ | D.①④ |
若(1+ )4=a+b
)4=a+b (a,b为有理数),则a+b=( )
(a,b为有理数),则a+b=( )
| A.33 | B.29 | C.23 | D.19 |
由0,1,2,3,…,9十个数字和一个虚数单位i,可以组成虚数的个数为( )
| A.100 | B.10 | C.9 | D.90 |
用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( ).
| A.243 | B.252 | C.261 | D.279 |