题目内容
定义一种运算：（a1，a2）?（a3，a4）=a1a4-a2a3，将函数f（x）=（
，2sinx）?（cosx，cos2x）的图象向左平移n（n＞0）个单位，所得图象对应的函数为偶函数，则n的最小值为
．
| 3 |
| 5π |
| 12 |
| 5π |
| 12 |
分析：利用新定义直接求出f（x）的表达式，图象向左平移n（n＞0）个单位，所得图象对应的函数为偶函数，
解答：解：因为（a1，a2）?（a3，a4）=a1a4-a2a3，
所以f（x）=（
，2sinx）?（cosx，cos2x）=
cos2x-2sinxcosx=2cos（2x+
），
它的图象向左平移n（n＞0）个单位，所得图象对应的函数为偶函数，函数为：f（x）=2cos（2x+2n+
）
所以 2n+
=π时，n最小，所以n的最小值为：
故答案为：
所以f（x）=（
| 3 |
| 3 |
| π |
| 6 |
它的图象向左平移n（n＞0）个单位，所得图象对应的函数为偶函数，函数为：f（x）=2cos（2x+2n+
| π |
| 6 |
所以 2n+
| π |
| 6 |
| 5π |
| 12 |
故答案为：
| 5π |
| 12 |
点评：本题是基础题，考查新定义，三角函数式的化简，图象平移，三角函数的性质，考查计算能力，分析问题解决问题的能力．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
，2sinx）?（cosx，cos2x）的图象向左平移n（n＞0）个单位，所得图象对应的函数为偶函数，则n的最小值为________．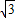
，2sinx）?（cosx，cos2x）的图象向左平移n（n＞0）个单位，所得图象对应的函数为偶函数，则n的最小值为 ．
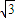，2sinx）?（cosx，cos2x）的图象向左平移n（n＞0）个单位，所得图象对应的函数为偶函数，则n的最小值为 ．