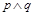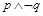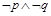题目内容
设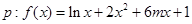 在
在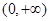 内单调递增,
内单调递增,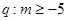 ,则
,则 是
是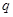 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:设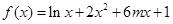 在
在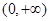 内单调递增,
内单调递增,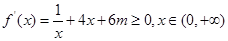 恒成立,即
恒成立,即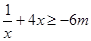 在
在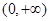 内恒成立,而
内恒成立,而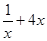 在
在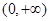 内的最小值为
内的最小值为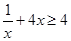 ,即
,即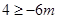 ,可得
,可得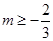 ,从而
,从而 ,故
,故 是
是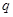 的充分不必要条件.
的充分不必要条件.
考点:充要条件的判断.

练习册系列答案
相关题目
若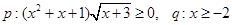 ,则p是q的 ( )
,则p是q的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列有关命题的说法中错误的是( )
A.对于命题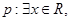 使得 使得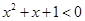 ,则 ,则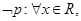 均有 均有 |
B. 是 是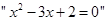 的充分不必要条件 的充分不必要条件 |
C.命题“若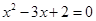 ,则 ,则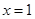 “的逆否命题为: “若 “的逆否命题为: “若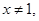 则 则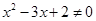 ” ” |
D.若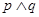 为假命题,则 为假命题,则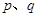 均为假命题 均为假命题 |
“函数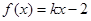 在区间
在区间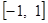 上存在零点”是“
上存在零点”是“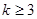 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“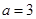 ”是“函数
”是“函数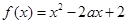 在区间
在区间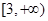 内单调递增”的( )
内单调递增”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题:
(1)“若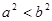 ,则
,则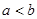 ”的逆命题;
”的逆命题;
(2)“全等三角形面积相等”的否命题;
(3)“若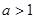 ,则
,则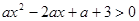 的解集为R”的逆否命题;
的解集为R”的逆否命题;
(4)“若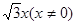 为有理数,则
为有理数,则 为无理数”。
为无理数”。
其中正确的命题是 ( )
| A.(3)(4) | B.(1)(3) | C.(1)(2) | D.(2)(4) |
下列给出的四个命题中,说法正确的是( )
A.命题“若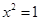 ,则 ,则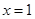 ”的否命题是“若 ”的否命题是“若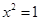 ,则 ,则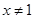 ”; ”; |
B.“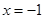 ”是“ ”是“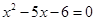 ”的必要不充分条件; ”的必要不充分条件; |
C.命题“存在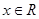 ,使得 ,使得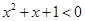 ”的否定是“对任意 ”的否定是“对任意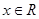 ,均有 ,均有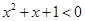 ”; ”; |
D.命题“若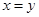 ,则 ,则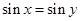 ”的逆否命题为真. ”的逆否命题为真. |
命题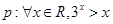 ;命题
;命题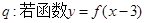 为奇函数 , 则
为奇函数 , 则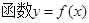 的图像关于点
的图像关于点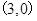 成中心对称,下列命题正确的是( )
成中心对称,下列命题正确的是( )
A.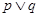 真 真 | B. 真 真 | C.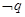 真 真 | D.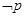 假 假 |
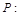 不等式
不等式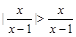 的解集为
的解集为 ;命题
;命题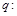 在
在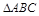 中“
中“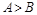 ”是“
”是“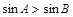 ”成立的必要充分条件,则下列命题为真命题的为 ( )
”成立的必要充分条件,则下列命题为真命题的为 ( )