题目内容
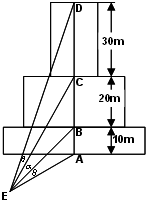
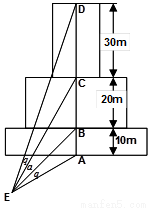
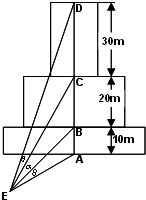
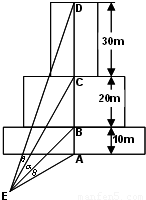
如图为一建筑物的正视图，尺寸如图中标出，为了做好火灾的防备工作，需要在地面上确定安装喷水枪的地点E，经测试只有当∠AEB=∠CED（图中的θ角）时，才能使得水枪喷射能够覆盖整个建筑物，求水枪安装点E到建筑物的距离EA长．（注：图中A，B，C，D，E在同一个平面内；不考虑喷水枪的高度．）
分析：设EA=xm，分别求得Rt△ABE中tanθ=
，Rt△ACE中，tan(θ+a)=
，Rt△ADE中，tan（2θ+a）=
，根据tan（2θ+a）=tan[θ+（θ+a）]=
，可建立方程，从而可求水枪安装点E到建筑物距离．
| 10 |
| x |
| 30 |
| x |
| 60 |
| x |
| tanθ+tan(θ+a) |
| 1-tanθtan(θ+a) |
解答：解：设EA=xm，则DA⊥AE
在Rt△ABE中，tanθ=
，在Rt△ACE中，tan(θ+a)=
在Rt△ADE中，tan（2θ+a）=
∵tan（2θ+a）=tan[θ+（θ+a）]=
=
=
∴
=
∴x2=900
∴x=30
答：水枪安装点E到建筑物距离为30m．
在Rt△ABE中，tanθ=
| 10 |
| x |
| 30 |
| x |
在Rt△ADE中，tan（2θ+a）=
| 60 |
| x |
∵tan（2θ+a）=tan[θ+（θ+a）]=
| tanθ+tan(θ+a) |
| 1-tanθtan(θ+a) |
| ||||
1-
|
| 40x |
| x2-300 |
∴
| 40x |
| x2-300 |
| 60 |
| x |
∴x2=900
∴x=30
答：水枪安装点E到建筑物距离为30m．
点评：本题考查利用三角函数解决实际问题，考查角的变换，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
，经测试只有当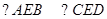
（图中的
角）时，才能使得水枪喷射能够覆盖整个建筑物，求水枪安装点
长．（注：图中
在同一个平面内；不考虑喷水枪的高度．）
，经测试只有当
（图中的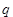
角）时，才能使得水枪喷射能够覆盖整个建筑物，求水枪安装点
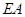长．（注：图中
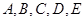在同一个平面内；不考虑喷水枪的高度．）
