题目内容
已知 .则cos(α-β)的值为
.则cos(α-β)的值为
- A.

- B.

- C.

- D.

A
分析:把两个条件平方相加,再利用两角差的余弦公式求得cos(α-β)的值.
解答:∵已知 ,平方可得
,平方可得
cos2α+2cosαcosβ+cos2β= ①,sin2α+2sinαsinβ+sin2β=
①,sin2α+2sinαsinβ+sin2β= ②.
②.
把①和②相加可得 2+2cosαcosβ+2sinαsinβ=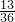 ,即 2+2cos(α-β)=
,即 2+2cos(α-β)=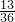 ,
,
解得cos(α-β)= ,
,
故选A.
点评:本题主要考查同角三角函数的基本关系,两角差的余弦公式的应用,属于中档题.
分析:把两个条件平方相加,再利用两角差的余弦公式求得cos(α-β)的值.
解答:∵已知
 ,平方可得
,平方可得cos2α+2cosαcosβ+cos2β=
 ①,sin2α+2sinαsinβ+sin2β=
①,sin2α+2sinαsinβ+sin2β= ②.
②.把①和②相加可得 2+2cosαcosβ+2sinαsinβ=
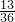 ,即 2+2cos(α-β)=
,即 2+2cos(α-β)=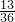 ,
,解得cos(α-β)=
 ,
,故选A.
点评:本题主要考查同角三角函数的基本关系,两角差的余弦公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目