题目内容
两个人射击,甲射击一次中靶概率是
,乙射击一次中靶概率是
,
(1)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(2)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(3)两人各射击5次,是否有99%的把握断定他们至少中靶一次?
| 1 |
| 2 |
| 1 |
| 3 |
(1)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(2)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(3)两人各射击5次,是否有99%的把握断定他们至少中靶一次?
分析:(1)两人各射击一次,中靶至少一次就算完成目标,分成三种情况①乙中靶甲不中②甲中靶乙不中③甲乙全中,分别计算三种情况的概率,即可得到答案;
(2)两人各射击2次,中靶至少3次就算完成目标,分成两类情况,共击中3次和共击中4次,分别计算出每一类的概率,相加后,即可得到答案;
(3)我们可计算出两人各射击5次均不中的概率,进而根据对立事件概率减法公式,求出两人各射击5次,至少中靶一次的概率,比照后即可得到答案.
(2)两人各射击2次,中靶至少3次就算完成目标,分成两类情况,共击中3次和共击中4次,分别计算出每一类的概率,相加后,即可得到答案;
(3)我们可计算出两人各射击5次均不中的概率,进而根据对立事件概率减法公式,求出两人各射击5次,至少中靶一次的概率,比照后即可得到答案.
解答:解:(Ⅰ)共三种情况:乙中靶甲不中
•
=
; 甲中靶乙不中
•
=
;
甲乙全中
•
=
.∴概率是
+
+
=
.
(Ⅱ)两类情况:
共击中3次
(
)2(
)0×
(
)1(
)1+
(
)1(
)1×
(
)2(
)0=
;
共击中4次
(
)2(
)0×
(
)2(
)0=
,∴概率为
+
=
.
(III)1-
(
)5
(
)5=1-
=
>0.99,能断定
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
甲乙全中
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
| 2 |
| 3 |
(Ⅱ)两类情况:
共击中3次
| C | 2 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
共击中4次
| C | 2 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 36 |
| 1 |
| 6 |
| 1 |
| 36 |
| 7 |
| 36 |
(III)1-
| C | 0 5 |
| 1 |
| 2 |
| C | 0 5 |
| 2 |
| 3 |
| 1 |
| 243 |
| 242 |
| 243 |
点评:本题考查的知识点互斥事件的概率加法公式,对立事件的概率减法公式,n次独立重复试验中恰好发生k次的概率,在处理此类问题是,型清楚所求事件之间的关系,及所求事件是分类的(分几类?)还是分步的(分几步?)是解答的关键

练习册系列答案
相关题目
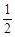 ,乙射击一次中靶概率是
,乙射击一次中靶概率是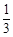 ,
,