题目内容
若A为抛物线 的顶点,过抛物线焦点的直线交抛物线于B、C两点,则
的顶点,过抛物线焦点的直线交抛物线于B、C两点,则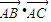 等于 .
等于 .
【答案】分析:题意可得,A(0,0),抛物线的焦点(0,1),则可得直线BC的方程为:y=kx+1
联立方程 可得
可得 设A(x1,y1)B(x1,y1),
设A(x1,y1)B(x1,y1),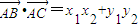 ,根据方程的根与系数的关系可求
,根据方程的根与系数的关系可求
解答:解:题意可得,A(0,0),抛物线的焦点(0,1)
则可得直线BC的方程为:y=kx+1
联立方程 可得
可得
设A(x1,y1)B(x1,y1),
则x1+x2=4k,x1x2=-4,y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1
 =(1+k2)x1x2+k(x1+x2)+1=-4(1+k2)+k•4k+1=-3
=(1+k2)x1x2+k(x1+x2)+1=-4(1+k2)+k•4k+1=-3
故答案为:-3

点评:本题主要考查了直线与抛物线的位置关系的应用,处理的一般思路是联立方程,根据方程的根与系数的关系进行求解.
联立方程
 可得
可得 设A(x1,y1)B(x1,y1),
设A(x1,y1)B(x1,y1),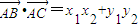 ,根据方程的根与系数的关系可求
,根据方程的根与系数的关系可求解答:解:题意可得,A(0,0),抛物线的焦点(0,1)
则可得直线BC的方程为:y=kx+1
联立方程
 可得
可得
设A(x1,y1)B(x1,y1),
则x1+x2=4k,x1x2=-4,y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1
 =(1+k2)x1x2+k(x1+x2)+1=-4(1+k2)+k•4k+1=-3
=(1+k2)x1x2+k(x1+x2)+1=-4(1+k2)+k•4k+1=-3故答案为:-3

点评:本题主要考查了直线与抛物线的位置关系的应用,处理的一般思路是联立方程,根据方程的根与系数的关系进行求解.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 的顶点,过抛物线焦点的直线交抛物线于B、C两点,则
的顶点,过抛物线焦点的直线交抛物线于B、C两点,则 等于________.
等于________.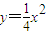 的顶点,过抛物线焦点的直线交抛物线于B、C两点,则
的顶点,过抛物线焦点的直线交抛物线于B、C两点,则 等于 .
等于 .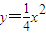 的顶点,过抛物线焦点的直线交抛物线于B、C两点,则
的顶点,过抛物线焦点的直线交抛物线于B、C两点,则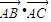 等于 .
等于 .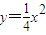 的顶点,过抛物线焦点的直线交抛物线于B、C两点,则
的顶点,过抛物线焦点的直线交抛物线于B、C两点,则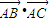 等于 .
等于 .