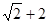题目内容
过双曲线 的一个焦点作一条渐近线的垂线,垂足恰好落在曲线
的一个焦点作一条渐近线的垂线,垂足恰好落在曲线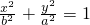 上,则双曲线的离心率为
上,则双曲线的离心率为
- A.

- B.

- C.

- D.2
C
分析:先分别求得双曲线的一渐近线,进而可推知过焦点的垂线的方程,与渐近线方程联立求得x和y,代入椭圆方程方程即可求得a和c的关系,求得离心率.
解答:双曲线一条渐近线方程为y= x,过焦点的垂线方程y=
x,过焦点的垂线方程y= (x-c)联立
(x-c)联立
解得 x= ,y=
,y=
把x y 代入椭圆方程得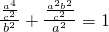
整理得可得e= =
=
故选C
点评:本题主要考查了椭圆的简单性质.考查了双曲线离心率的问题.
分析:先分别求得双曲线的一渐近线,进而可推知过焦点的垂线的方程,与渐近线方程联立求得x和y,代入椭圆方程方程即可求得a和c的关系,求得离心率.
解答:双曲线一条渐近线方程为y=
 x,过焦点的垂线方程y=
x,过焦点的垂线方程y= (x-c)联立
(x-c)联立解得 x=
 ,y=
,y=
把x y 代入椭圆方程得
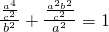
整理得可得e=
 =
=
故选C
点评:本题主要考查了椭圆的简单性质.考查了双曲线离心率的问题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
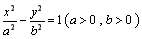

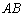
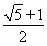
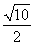
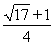
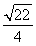
 的一个焦点
的一个焦点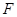 作双曲线的一条渐近线的垂线,垂足为
作双曲线的一条渐近线的垂线,垂足为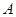 点,且与另一条渐近线交于点
点,且与另一条渐近线交于点 ,若
,若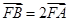 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )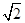 B.
B.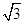 C.
C.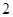 D.
D.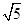
 作垂直于实轴的弦
作垂直于实轴的弦 ,
,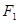 是另一焦点,若∠
是另一焦点,若∠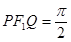 ,则双曲线的离心率
,则双曲线的离心率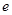 等于
等于 B.
B.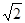 C.
C.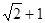 D.
D.