题目内容
若点P在曲线y=x3-3x2+(3-| 3 |
| 3 |
| 4 |
分析:先求出函数的导数y′的解析式,通过导数的解析式确定导数的取值范围,再根据函数的导数就是函数在此点的切线的斜率,来求出倾斜角的取值范围.
解答:解:∵函数的导数y′=3x2-6x+3-
=3(x-1)2-
≥-
,
∴tanα≥-
,又 0≤α<π,
∴0≤α<
或
≤α<π,
故答案为[0,
)∪[
,π).
| 3 |
| 3 |
| 3 |
∴tanα≥-
| 3 |
∴0≤α<
| π |
| 2 |
| 2π |
| 3 |
故答案为[0,
| π |
| 2 |
| 2π |
| 3 |
点评:此题考查了利用导数研究曲线上某点切线的方程,直线倾斜角与斜率的关系,以及正切函数的图象与性质.要求学生掌握导函数在某点的函数值即为过这点切线方程的斜率,且直线的斜率为倾斜角的正切值,掌握正切函数的图象与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若点P在曲线y=x3-3x2+(3-
)x+
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
| 3 |
| 3 |
| 4 |
A、[0,
| ||||||
B、[0,
| ||||||
C、[
| ||||||
D、[0,
|
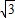 )x+
)x+ 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )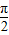 )
)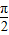 )∪[
)∪[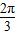 ,π)
,π)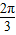 ,π)
,π)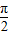 )∪(
)∪(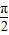 ,
,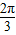 ]
]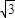 )x+
)x+ 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )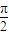 )
)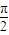 )∪[
)∪[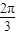 ,π)
,π)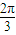 ,π)
,π)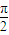 )∪(
)∪(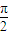 ,
,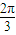 ]
]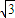 )x+
)x+ 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )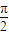 )
)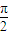 )∪[
)∪[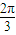 ,π)
,π)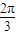 ,π)
,π)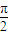 )∪(
)∪(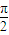 ,
,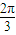 ]
]