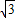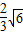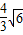题目内容
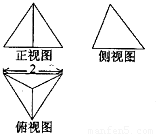
如图是各条棱长均为2的正四面体的三视图，则正（主）视图三角形的面积为（ ）
A．
B．2
C．
D．
【答案】分析：由题意及图可得知，此主视图是一个底边长为2，高为正四面体的高的等腰三角形，故可先求出正四面体的高，再其其面积选正确选项
解答：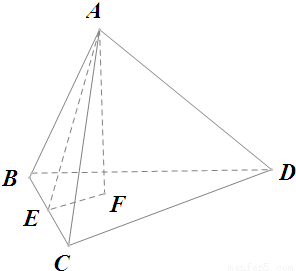
解：由题意及图可知，主视图是一个底边长为2，高等于正四面体的高的等腰三角形，下求正四面体的高
如图，正四面体A-BCD中，E是BC的中点，AF是正四面体的高
又正四面体边长是2，故可得AE=DE=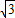
，
又F是A在底面的投影，所以EF=
DE=
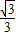
在直角三角形AFE中，可得AF=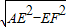
=
=
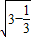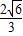
故主视图的面积是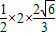
=
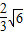
故选C
点评：本题考查简单几何体的三视图，此类题的关键是能由实物图得到正确的三视图或者由三视图可准确还原实物图
解答：
解：由题意及图可知，主视图是一个底边长为2，高等于正四面体的高的等腰三角形，下求正四面体的高如图，正四面体A-BCD中，E是BC的中点，AF是正四面体的高
又正四面体边长是2，故可得AE=DE=
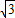，又F是A在底面的投影，所以EF=
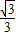
DE=在直角三角形AFE中，可得AF=
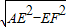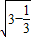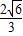
==故主视图的面积是
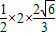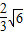
=故选C
点评：本题考查简单几何体的三视图，此类题的关键是能由实物图得到正确的三视图或者由三视图可准确还原实物图
练习册系列答案
相关题目
（2012•浙江模拟）如图是各条棱长均为2的正四面体的三视图，则正（主）视图三角形的面积为（ ）
如图，已知正三棱柱ABC-A1B1C1的各条棱长均为2，M是BC的中点．
