题目内容
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中 以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:
| 视力数据 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
| 人数 | 2 | 2 | 2 | 1 | 1 |
(2)已知其余五个班学生视力的平均值分别为4.3、4.4,4.5、4.6、4.8.若从这六个 班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.
【答案】分析:(1)把高三(1)班这8个学生的视力值相加,再除以8,即得学生视力的平均值.
(2)从这六个 班中任意抽取两个班学生视力的平均值作比较,所有的取法共有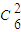 种,用列举法求得抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有10种,由此求得抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.
种,用列举法求得抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有10种,由此求得抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.
解答:解:(1)高三(1)班学生视力的平均值为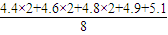 =4.7,
=4.7,
故用上述样本数据估计高三(1)班学生视力的平均值为 4.7.
(2)从这六个 班中任意抽取两个班学生视力的平均值作比较,所有的取法共有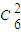 =15种,而满足抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有
=15种,而满足抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有
(4.3,4.4)、(4.3,4.5)、(4.4,4.5)、(4.4,4.6)、(4.5,4.6)、(4.5,4.7)、(4.6,4.7)、(4.6,4.8)、(4.7,4.8)、(4.7,4.8),共有10个,故抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率为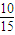 =
= .
.
点评:本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想,属于基础题.
(2)从这六个 班中任意抽取两个班学生视力的平均值作比较,所有的取法共有
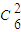 种,用列举法求得抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有10种,由此求得抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.
种,用列举法求得抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有10种,由此求得抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.解答:解:(1)高三(1)班学生视力的平均值为
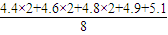 =4.7,
=4.7,故用上述样本数据估计高三(1)班学生视力的平均值为 4.7.
(2)从这六个 班中任意抽取两个班学生视力的平均值作比较,所有的取法共有
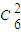 =15种,而满足抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有
=15种,而满足抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有(4.3,4.4)、(4.3,4.5)、(4.4,4.5)、(4.4,4.6)、(4.5,4.6)、(4.5,4.7)、(4.6,4.7)、(4.6,4.8)、(4.7,4.8)、(4.7,4.8),共有10个,故抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率为
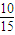 =
= .
.点评:本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:
|
视力数据 |
4.0 |
4.1 |
4.2 |
4.3 |
4.4 |
4.5 |
4.6 |
4.7 |
4.8 |
4.9 |
5.0 |
5.1 |
5.2 |
5.3 |
|
人数 |
|
|
|
|
2 |
|
2 |
|
2 |
1 |
|
1 |
|
|
(1)用上述样本数据估计高三(1)班学生视力的平均值;
(2)已知其余五个班学生视力的平均值分别为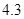 、
、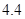 、
、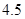 、
、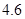 、
、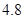 .若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于
.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于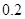 的概率.
的概率.
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中 以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三
(1)班抽取的8名学生的视力数据与人数见下表:
| 视力数据 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
| 人数 | 2 | 2 | 2 | 1 | 1 |
(2)已知其余五个班学生视力的平均值分别为4.3、4.4,4.5、4.6、4.8.若从这六个 班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.