题目内容
在空间中有互异的四个点A、B、C、D，存在不全为零的实数x和y使得
=x
+y
成立，但x+y≠1，又(
+
-2
)•(
-
)=0，则A、B、C三点围成图形的形状一定为（ ）
| DA |
| DB |
| DC |
| DB |
| DC |
| DA |
| AB |
| AC |
| A、直角三角形 | B、线段 |
| C、等腰三角形 | D、正三角形 |
分析：根据向量共线的性质，依题意推断出A、B、C三点不共线，利用向量积的性质推断出
2=
2进而可判断出AB=AC，
| AB |
| AC |
解答：解：∵
=x
+y
，但x+y≠1
∴A、B、C三点不共线，
∵(
+
-2
)•(
-
)=0
∴
2=
2
∴AB=AC，
∴一定为等腰三角形．
故选C
| DA |
| DB |
| DC |
∴A、B、C三点不共线，
∵(
| DB |
| DC |
| DA |
| AB |
| AC |
∴
| AB |
| AC |
∴AB=AC，
∴一定为等腰三角形．
故选C
点评：本题主要考查了平面向量的基本知识，三角形形状的判断．考查了学生对基础知识的综合运用．
练习册系列答案
阅读快车系列答案
相关题目
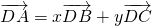成立，但x+y≠1，又
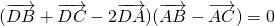，则A、B、C三点围成图形的形状一定为
成立，但x+y≠1，又
，则A、B、C三点围成图形的形状一定为（ ）