题目内容
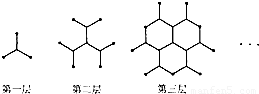
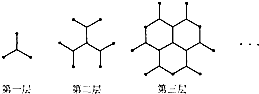 一种平面分形图的形成过程如图所示,第一层是同 一点出发的三条线段,长度均为1,每两条线段夹角为 120°;第二层是在第一层的每一条线段末端,再生成 两条与该线段成120°角的线段,长度不变;第三层按 第二层的方法再在第二层每一条线段的末端各生成两条 线段;重复前面的作法,直至第6层,则分形图第6层 各条线段末端之间的距离的最大值为________.
一种平面分形图的形成过程如图所示,第一层是同 一点出发的三条线段,长度均为1,每两条线段夹角为 120°;第二层是在第一层的每一条线段末端,再生成 两条与该线段成120°角的线段,长度不变;第三层按 第二层的方法再在第二层每一条线段的末端各生成两条 线段;重复前面的作法,直至第6层,则分形图第6层 各条线段末端之间的距离的最大值为________.
6
分析:分析图形可知,左右两端的两个点为各条线段末端之间的距离的最大值.再根据30°直角三角形的性质、等腰三角形的性质分别计算前三个图形中的距离,进一步推而广之.
解答: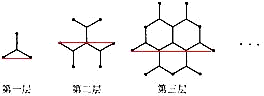 解:第一层的左右两端的两个点的距离为
解:第一层的左右两端的两个点的距离为 ;
;
第二层的左右两端的两个点的距离为2 ;
;
第三层的左右两端的两个点的距离为3 ;
;
第四层的左右两端的两个点的距离为4 ;
;
…
推而广之,则第6层的左右两端的两个点的距离为6 .
.
而各层各条线段末端之间的距离的最大值为的左右两端的两个点的距离.
即分形图第6层 各条线段末端之间的距离的最大值为 6 .
.
故答案为6 .
.
点评:此题考查了简单的合情推理,综合运用了等腰三角形的性质、30°直角三角形的性质以及数的计算.

分析:分析图形可知,左右两端的两个点为各条线段末端之间的距离的最大值.再根据30°直角三角形的性质、等腰三角形的性质分别计算前三个图形中的距离,进一步推而广之.
解答:
 解:第一层的左右两端的两个点的距离为
解:第一层的左右两端的两个点的距离为 ;
;第二层的左右两端的两个点的距离为2
 ;
;第三层的左右两端的两个点的距离为3
 ;
;第四层的左右两端的两个点的距离为4
 ;
;…
推而广之,则第6层的左右两端的两个点的距离为6
 .
.而各层各条线段末端之间的距离的最大值为的左右两端的两个点的距离.
即分形图第6层 各条线段末端之间的距离的最大值为 6
 .
.故答案为6
 .
.点评:此题考查了简单的合情推理,综合运用了等腰三角形的性质、30°直角三角形的性质以及数的计算.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
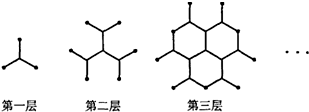 (2013•宁德模拟)一种平面分形图的形成过程如图所示,第一层是同 一点出发的三条线段,长度均为1,每两条线段夹角为 120°;第二层是在第一层的每一条线段末端,再生成 两条与该线段成120°角的线段,长度不变;第三层按 第二层的方法再在第二层每一条线段的末端各生成两条 线段;重复前面的作法,直至第6层,则分形图第6层 各条线段末端之间的距离的最大值为
(2013•宁德模拟)一种平面分形图的形成过程如图所示,第一层是同 一点出发的三条线段,长度均为1,每两条线段夹角为 120°;第二层是在第一层的每一条线段末端,再生成 两条与该线段成120°角的线段,长度不变;第三层按 第二层的方法再在第二层每一条线段的末端各生成两条 线段;重复前面的作法,直至第6层,则分形图第6层 各条线段末端之间的距离的最大值为