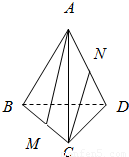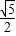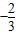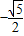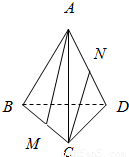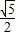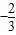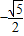题目内容
已知正四面体A-BCD,它的内切球(与四个面都相切的球)半径为r,外接球(过正四面体的四个顶点的球)的半径为R,则
=
| R | r |
3
3
.分析:作出正四面体A-BCD的高DE,延长CE,交AB于G,连接DG,过C作DG边上的高CF.在△CDG中加以研究,可得DE、CF的交点I就是内切球和外接球公共的球心,设正四面体棱长为1,可算出CE、GE、ED的长,利用Rt△DEG∽Rt△CEI得线段成比例,从而得出EI=
,DI=
,由此不难得到R与r的比值.
| ||
| 12 |
| ||
| 4 |
解答:解:过点D作DE⊥平面ABC,垂足为E,则E是正三角形ABC的中心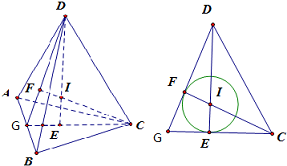
则根据球的对称性和正四面体的性质,得外接球和内切球的球心在同一点处,设为I,则I在高线DE上
延长CE,交AB于G,连接DG,过C作DG边上的高CF,则I在CF上
I到平面ABC的距离IE等于内切球半径r,ID=IC=R是外接球半径
设正四面体棱长为1,则
正△ABC中,CG=
,CE=
CG═
,GE=
CG=
,
Rt△DEG中,DG=CG=
,可得DE=
=
∵Rt△DEG∽Rt△CEI,
∴
=
,即
=
,可得EI=
,所以ID=DE-EI=
即r=
,R=
,可得
=
=3
故答案为:3

则根据球的对称性和正四面体的性质,得外接球和内切球的球心在同一点处,设为I,则I在高线DE上
延长CE,交AB于G,连接DG,过C作DG边上的高CF,则I在CF上
I到平面ABC的距离IE等于内切球半径r,ID=IC=R是外接球半径
设正四面体棱长为1,则
正△ABC中,CG=
| ||
| 2 |
| 2 |
| 3 |
| ||
| 3 |
| 1 |
| 3 |
| ||
| 6 |
Rt△DEG中,DG=CG=
| ||
| 2 |
| DG2-GE2 |
| ||
| 3 |
∵Rt△DEG∽Rt△CEI,
∴
| EG |
| EI |
| DE |
| CE |
| ||||
| EI |
| ||||
|
| ||
| 12 |
| ||
| 4 |
即r=
| ||
| 12 |
| ||
| 4 |
| R |
| r |
| ||||
|
故答案为:3
点评:本题给出正四面体的外接球与内切球,求它们的半径之比,着重考查了正四面体的性质和球的内接、外切几何体等知识,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 已知正四面体ABCD中,M、N分别是BC和AD中点,则异面直线AM和CN所成的角的正切值为( )
已知正四面体ABCD中,M、N分别是BC和AD中点,则异面直线AM和CN所成的角的正切值为( )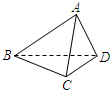 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.