题目内容
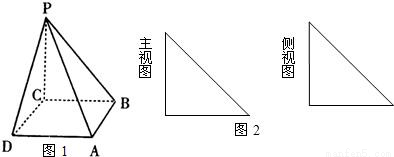
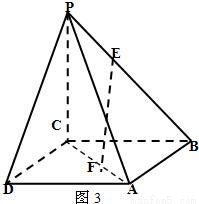
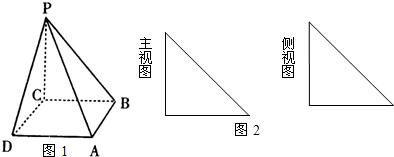
如下图,在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图1),图2为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.(Ⅰ)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面
图形的面积.
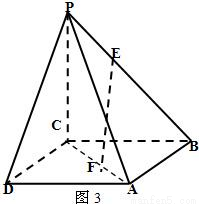
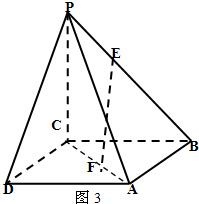
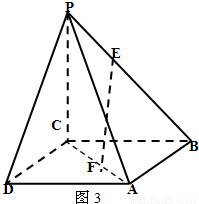
(Ⅱ)图3中,E为棱PB上的点,F为底面对角线AC上的点,且
 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.
【答案】分析:根据图形可很容易画出俯视图.第二问要求证线面平行,先证线线平行再证线面平行(注意辅助线的利用).
解答:解:(Ⅰ)(1)该四棱锥相应的俯视图为内含对角线、边长为6cm的正方形如图;(2分)
 (4分)
(4分)
其面积为6×6=36(cm2).(6分)
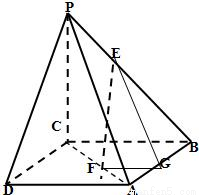 (Ⅱ)在三角形PAB中,过E作EG∥PA,EG交AB于G,连接FG.(7分)
(Ⅱ)在三角形PAB中,过E作EG∥PA,EG交AB于G,连接FG.(7分)
依题意:BE:EP=BG:GA=CF:FA故在三角形BCA中,FG∥BC,
在正方形ABCD中,AD∥BC,所以FG∥AD.(8分)
又FG?平面PDA,所以,FG∥平面PDA,(10分)
同理EG∥平面PDA.(11分)
由FG与EG相交,得平面EFG∥平面PDA,(12分)
又EF在平面EFG内,所以直线EF与平面PDA没有公共点
所以EF∥平面PDA.(13分)
点评:本题考查学生的空间想象能力,以及线线、线面之间关系的证明,是中档题.
解答:解:(Ⅰ)(1)该四棱锥相应的俯视图为内含对角线、边长为6cm的正方形如图;(2分)
 (4分)
(4分)其面积为6×6=36(cm2).(6分)
 (Ⅱ)在三角形PAB中,过E作EG∥PA,EG交AB于G,连接FG.(7分)
(Ⅱ)在三角形PAB中,过E作EG∥PA,EG交AB于G,连接FG.(7分)依题意:BE:EP=BG:GA=CF:FA故在三角形BCA中,FG∥BC,
在正方形ABCD中,AD∥BC,所以FG∥AD.(8分)
又FG?平面PDA,所以,FG∥平面PDA,(10分)
同理EG∥平面PDA.(11分)
由FG与EG相交,得平面EFG∥平面PDA,(12分)
又EF在平面EFG内,所以直线EF与平面PDA没有公共点
所以EF∥平面PDA.(13分)
点评:本题考查学生的空间想象能力,以及线线、线面之间关系的证明,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
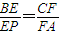 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.
 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.

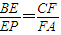 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.