题目内容
过平面区域 内一点
内一点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为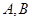 ,记
,记 ,则当
,则当 最小时
最小时 的值为( )
的值为( )
A.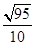 | B. | C. | D. |
C
解析试题分析:因为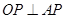 ,所以在
,所以在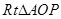 中
中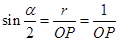 ,
,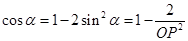 ,因为
,因为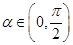 ,而函数
,而函数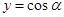 在
在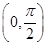 上是减函数,所以当
上是减函数,所以当 最小时
最小时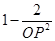 最大,因为
最大,因为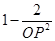 为增函数则此时
为增函数则此时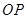 最大。根据不等式表示的可行域可知当
最大。根据不等式表示的可行域可知当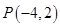 时
时 。综上可得
。综上可得 最小时
最小时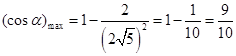 。故C正确。
。故C正确。
考点:1二倍角公式;2直线与圆相切;3函数的单调性。

练习册系列答案
相关题目
已知 是第二象限角,且
是第二象限角,且 ,则
,则 的值为( ).
的值为( ).
A. | B. | C. | D. |
已知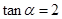 ,
,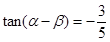 ,则
,则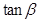 等于( )
等于( )
A.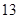 | B.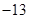 | C.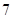 | D. |
在平面坐标系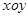 中,直线
中,直线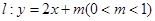 与圆
与圆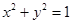 相交于
相交于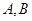 ,(
,(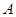 在第一象限)两个不同的点,且
在第一象限)两个不同的点,且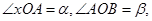 则
则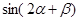 的值是 ( )
的值是 ( )
A.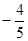 | B. | C.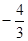 | D.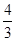 |
已知锐角 满足
满足 则
则 ( )
( )
A. | B. | C.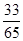 | D. |
函数y=sin( +x)cos(
+x)cos( -x)的最大值为( )
-x)的最大值为( )
A. |
B. |
C. |
D. |
[2012·湖南高考]函数f(x)=sinx-cos(x+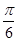 )的值域为( )
)的值域为( )
| A.[-2,2] | B.[-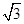 , ,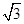 ] ] |
| C.[-1,1] | D.[-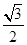 , ,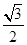 ] ] |
 .
. 的最小值和最小正周期;
的最小值和最小正周期; 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值. ),满足tan(α+β)=4tanβ,则tanα的最大值是( )
),满足tan(α+β)=4tanβ,则tanα的最大值是( )


