题目内容
若函数y=lnx与y=
的图象的交点为(x0,y0),则x0所在的区间是( )
| 2 |
| x |
| A、(1,2) |
| B、(2,3) |
| C、(e,3) |
| D、(e,+∞) |
分析:由已知,可将问题转化为函数f(x)=lnx-
零点所在的区间问题.利用零点存在性定理.
| 2 |
| x |
解答:解:有题可知,x0是函数f(x)=lnx-
的零点,
∵f(2)=ln2-
=ln2-1<0,f(e)=lne-
=1-
>0,f(3)>0,∴x0所在的区间是(2,3)
故选B.
| 2 |
| x |
∵f(2)=ln2-
| 2 |
| 2 |
| 2 |
| e |
| 2 |
| e |
故选B.
点评:本题考查的是零点存在的大致区间问题.在解答的过程当中充分体现了函数零点存在性定理的知识以及问题转化的思想.值得体会反思.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 的图象的交点为(x0,y0),则x0所在的区间是
的图象的交点为(x0,y0),则x0所在的区间是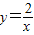 的图象的交点为(x,y),则x所在的区间是( )
的图象的交点为(x,y),则x所在的区间是( )