题目内容
20、给假设小王家订了一份报纸，送报人可能在早上6点-8点之间把报纸送到你家，小王每天离家去工作的时间在早上7点-9点之间．
（1）设事件A：小王离家前不能看到报纸．设送报人到达的时间为x，小王离家去工作的时间为y，写出x，y 的范围和事件A与x，y的关系．
（2）求事件A发生的概率是多少？（必须有过程）
（1）设事件A：小王离家前不能看到报纸．设送报人到达的时间为x，小王离家去工作的时间为y，写出x，y 的范围和事件A与x，y的关系．
（2）求事件A发生的概率是多少？（必须有过程）
分析：（1）送报人到达的时间为x，大王离家去工作的时间为y．（x，y）可以看成平面中的点试验的全部结果所构成的区域为Ω=（x，y|6≤x≤8，7≤y≤9是一个矩形区域，事件A表示大王离家前不能看到报纸，所构成的区域为A={（x，y）∈Ω|x≥y}，
（2）作出符合题意的图象，由图根据几何概率模型的规则求解即可．
（2）作出符合题意的图象，由图根据几何概率模型的规则求解即可．
解答：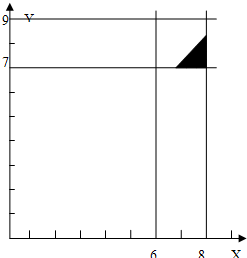
解：（1）设送报人到达的时间为X，小王离家去工作的时间为Y．
（X，Y）可以看成平面中的点，试验的全部结果所构成的区域为Ω={（X，Y）|6≤X≤8，7≤Y≤9}
一个正方形区域，面积为S1=4，事件A表示小王离家前不能看到报纸，
所构成的区域为：A={（X，Y）|6≤X≤8，7≤Y≤9，X≥Y}
即图中的阴影部分，面积为SA=0.5．
（2）由（1）知，这是一个几何概型，所以P（A）=SA/S1=0.5/4=0.125．
所以小王离家前不能看到报纸的概率是0.125．
解：（1）设送报人到达的时间为X，小王离家去工作的时间为Y．（X，Y）可以看成平面中的点，试验的全部结果所构成的区域为Ω={（X，Y）|6≤X≤8，7≤Y≤9}
一个正方形区域，面积为S1=4，事件A表示小王离家前不能看到报纸，
所构成的区域为：A={（X，Y）|6≤X≤8，7≤Y≤9，X≥Y}
即图中的阴影部分，面积为SA=0.5．
（2）由（1）知，这是一个几何概型，所以P（A）=SA/S1=0.5/4=0.125．
所以小王离家前不能看到报纸的概率是0.125．
点评：点评：本题考查几何概率模型与模拟方法估计概率，求解的关键是掌握两种求概率的方法的定义及规则，本题是一个基础题．
练习册系列答案
相关题目