题目内容
某分公司经销某种品牌的产品,每件产品的成本为3元,并且每件产品需向总公司交a(3≤a≤5)元的管理费,预计当每件产品的售价为x(9≤x≤11)元时,一年的销售量为(12-x)2万件.(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a).
分析:(1)根据题意先求出每件产品的利润,再乘以一年的销量,便可求出分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)根据L与x的函数关系式先求出该函数的导数,令L′(x)=0便可求出极值点,从而求出时最大利润,再根据a的取值范围分类讨论当a取不同的值时,最大利润各为多少.
(2)根据L与x的函数关系式先求出该函数的导数,令L′(x)=0便可求出极值点,从而求出时最大利润,再根据a的取值范围分类讨论当a取不同的值时,最大利润各为多少.
解答:解:(1)分公司一年的利润L(万元)与售价x的函数关系式为:
L=(x-3-a)(12-x)2,x∈[9,11].
(2)L′(x)=(12-x)2+2(x-3-a)(12-x)×(-1)=(12-x)2-2(x-3-a)(12-x)=(12-x)(18+2a-3x).
令L′(x)=0得x=6+
a或x=12(不合题意,舍去).
∵3≤a≤5,∴8≤6+
a≤
.
在x=6+
a两侧L′的值由正值变负值.
所以,当8≤6+
a≤9,即3≤a≤
时,
Lmax=L(9)=(9-3-a)(12-9)2=9(6-a);
当9<6+
a≤
,即
<a≤5时,
Lmax=L(6+
a)=(6+
a-3-a)[12-(6+
a)]2
=4(3-
a)3,
Q(a)=
即当3≤a≤
时,当每件售价为9元,分公司一年的利润L最大,最大值Q(a)=9(6-a)万元;
当
<a≤5时,当每件售价为(6+
a)元,分公司一年的利润L最大,最大值Q(a)=4(3-
a)3万元.
L=(x-3-a)(12-x)2,x∈[9,11].
(2)L′(x)=(12-x)2+2(x-3-a)(12-x)×(-1)=(12-x)2-2(x-3-a)(12-x)=(12-x)(18+2a-3x).
令L′(x)=0得x=6+
| 2 |
| 3 |
∵3≤a≤5,∴8≤6+
| 2 |
| 3 |
| 28 |
| 3 |
在x=6+
| 2 |
| 3 |
所以,当8≤6+
| 2 |
| 3 |
| 9 |
| 2 |
Lmax=L(9)=(9-3-a)(12-9)2=9(6-a);
当9<6+
| 2 |
| 3 |
| 28 |
| 3 |
| 9 |
| 2 |
Lmax=L(6+
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
=4(3-
| 1 |
| 3 |
Q(a)=
|
即当3≤a≤
| 9 |
| 2 |
当
| 9 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
点评:本题主要考查了函数的导数的求法以及利用导数来求得函数的最值问题,是各地高考的热点和难点,解题时注意自变量的取值范围以及分类讨论等数学思想的运用,属于中档题.

练习册系列答案
相关题目
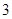 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交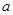 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件.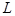 (万元)与每件产品的售价
(万元)与每件产品的售价 .
. 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元(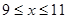 )时,一年的销售量为
)时,一年的销售量为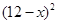 万件.
万件.  (万元)与每件产品的售价
(万元)与每件产品的售价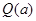 .ks.5u
.ks.5u