题目内容
一个四面体ABCD的所有棱的长度都为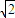 ,四个顶点A、B、C、D在同一球面上,则A、B两点的球面距离为 .
,四个顶点A、B、C、D在同一球面上,则A、B两点的球面距离为 .
【答案】分析:由题意求出外接球的半径,设球心为O,然后求出∠AOB的大小,即可求解其外接球球面上A、B两点间的球面距离.
解答: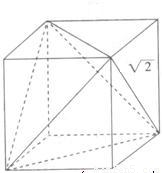 解:如图,将四面体补成正方体,则正方体的棱长是1,正方体的对角线长为:
解:如图,将四面体补成正方体,则正方体的棱长是1,正方体的对角线长为: ,
,
正四面体的外接球的半径为: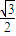 .
.
设球心为O.
∴cos∠AOB=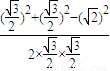 =-
=- ,
,
∴∠AOB=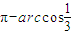 ,
,
外接球球面上A、B两点间的球面距离为: .
.
故答案为: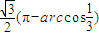
点评:本题考查正四面体的外接球的球面距离的求法,考查空间想象能力,计算能力.
解答:
 解:如图,将四面体补成正方体,则正方体的棱长是1,正方体的对角线长为:
解:如图,将四面体补成正方体,则正方体的棱长是1,正方体的对角线长为: ,
,正四面体的外接球的半径为:
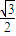 .
.设球心为O.
∴cos∠AOB=
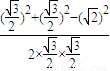 =-
=- ,
,∴∠AOB=
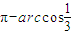 ,
,外接球球面上A、B两点间的球面距离为:
 .
.故答案为:
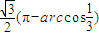
点评:本题考查正四面体的外接球的球面距离的求法,考查空间想象能力,计算能力.

练习册系列答案
相关题目
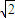 ,四个顶点A、B、C、D在同一球面上,则A、B两点的球面距离为 .
,四个顶点A、B、C、D在同一球面上,则A、B两点的球面距离为 .