题目内容
已知直线x+3y-7=0,kx-y-2=0和x轴、y轴围成四边形有外接圆,则实数k等于( )
| A.-3 | B.3 |
| C.-6 | D.6 |
B
解析考点:直线的一般式方程与直线的垂直关系.
分析:由直线x+3y-7=0和kx-y-2=0与x轴、y轴所围成的四边形有外接圆,得到对角之和为180°,
又∠AOB为90°,得到两直线的夹角为90°,即两直线垂直,根据两直线垂直时斜率的乘积为-1,分别表示出两直线的斜率相乘等于-1列出关于k的方程,求出的解即可得到实数k的值.
解:由图形可知:∠AOB=90°,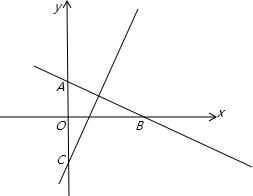
∴直线x+3y-7=0和kx-y-2=0的夹角为90°即两直线垂直,
又直线x+3y-7=0的斜率为-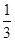 ,直线kx-y-2=0的斜率为k,
,直线kx-y-2=0的斜率为k,
则-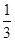 k=-1,解得k=3.
k=-1,解得k=3.
故选C.

练习册系列答案
相关题目
已知直线
x+3y-7=0,kx-y-2=0和x轴、y轴围成的四边形有外接圆,则实数k等于[
]|
A .-3 |
B .3 |
|
C .-6 |
D .6 |