题目内容
点A到图形C上每一个点的距离的最小值称为点A到图形C的距离.已知点A(1,0),圆C:x2+2x+y2=0,那么平面内到圆C的距离与到点A的距离之差为1的点的轨迹是( )A..双曲线的一支
B..椭圆
C.抛物线
D.射线
【答案】分析:由题设条件能够推导出动点M(x,y)到两定点A(1,0),C(-1,0)的距离之差为2,由|AC|=2,知点M的轨迹是射线.
解答:解:圆C:x2+2x+y2=0的圆心C(-1,0),半径r=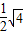 =1,
=1,
设平面内到圆C的距离与到点A的距离之差为1的点的坐标为M(x,y),
则(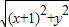 -1)-
-1)-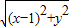 =1,
=1,
∴ -
-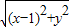 =2,
=2,
即动点M(x,y)到两定点A(1,0),C(-1,0)的距离之差为2,
∵|AC|=2,
∴点M的轨迹是射线.
故选D.
点评:本题考查点的轨迹方程的求法,解题时要认真审题,注意双曲线定义的灵活运用.
解答:解:圆C:x2+2x+y2=0的圆心C(-1,0),半径r=
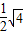 =1,
=1,设平面内到圆C的距离与到点A的距离之差为1的点的坐标为M(x,y),
则(
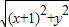 -1)-
-1)-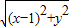 =1,
=1,∴
 -
-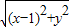 =2,
=2,即动点M(x,y)到两定点A(1,0),C(-1,0)的距离之差为2,
∵|AC|=2,
∴点M的轨迹是射线.
故选D.
点评:本题考查点的轨迹方程的求法,解题时要认真审题,注意双曲线定义的灵活运用.

练习册系列答案
相关题目