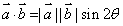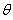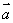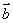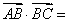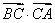题目内容
定义平面向量的正弦积为
•
=|
||
|sin2θ，（其中θ为
、
的夹角），已知△ABC中，
•
=
•
，则此三角形一定是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| AB |
| BC |
| BC |
| CA |
| A、等腰三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
分析：利用平面向量的正弦积可得csin2B=bsin2C，再利用正弦定理与二倍角的正弦可得cosB=cosC，从而可得答案．
解答：解：∵
•
=
•
，
∴casin2（π-B）=absin2（π-C），
∴csin2B=bsin2C，
由正弦定理与二倍角的正弦得：2sinBcosBsinC=2sinCcosCsinB，
∵B、C均为△ABC的内角，
∴sinB＞0，sinC＞0，
∴cosB=cosC，
∴B=C，
∴此三角形一定是等腰三角形，
故选：A．
| AB |
| BC |
| BC |
| CA |
∴casin2（π-B）=absin2（π-C），
∴csin2B=bsin2C，
由正弦定理与二倍角的正弦得：2sinBcosBsinC=2sinCcosCsinB，
∵B、C均为△ABC的内角，
∴sinB＞0，sinC＞0，
∴cosB=cosC，
∴B=C，
∴此三角形一定是等腰三角形，
故选：A．
点评：本题考查三角形的形状判断，考查平面向量的正弦积的应用，突出考查正弦定理与二倍角公式，属于中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
