题目内容
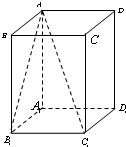 已知ABCD-A1B1C1D1是边长为1的正方体,求:
已知ABCD-A1B1C1D1是边长为1的正方体,求:(1)直线AC1与平面AA1B1B所成角的正切值;
(2)二面角B-AC1-D的大小;
(3)求点A到平面BDC1的距离.
分析:(1)连接AB1,说明AB1是AC1在平面AA1B1B上的射影,推出∠C1AB1就是AC1与平面AA1B1B所成的角,求出直线AC1与平面AA1B1B所成的角的正切值即可.
(2)过B作BE⊥AC1,垂足为E,连接ED,说明∠AEB是二面角B-AC1-D的平面角,在△DBE中,求出二面角B-AC1-D的大小即可.
(3)设点A到平面BDC1的距离为h,通过VA-BDC1=VC1-ABD=
S△ABD•CC1,与VA-BDC1=VC1-ABD=
S△C1AD•h,求出A到平面BDC1的距离.
(2)过B作BE⊥AC1,垂足为E,连接ED,说明∠AEB是二面角B-AC1-D的平面角,在△DBE中,求出二面角B-AC1-D的大小即可.
(3)设点A到平面BDC1的距离为h,通过VA-BDC1=VC1-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:(1)连接AB1,∵ABCD-A1B1C1D1是正方体
∴B1C1⊥平面AA1B1B,AB1是AC1在平面AA1B1B上的射影
∴∠C1AB1就是AC1与平面AA1B1B所成的角
在△C1AB1中,tan∠C1AB1=
=
∴直线AC1与平面AA1B1B所成的角的正切值为
.
(2)过B作BE⊥AC1,垂足为E,连接ED
∵△ABC1≌△ADC1,
∴∠BAC1=∠DAC1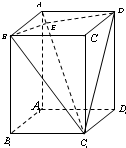
∵AB=AD,∠BAC1=∠DAC1,AE=AE
∴△ABE≌△ADE,
∴∠AEB=∠AED=
∴∠AEB是二面角B-AC1-D的平面角
在△DBE中,BE=ED=
,BD=
,
∴cos∠AEB=-
,即∠AEB=120°
∴二面角B-AC1-D的大小为120°.
(3)设点A到平面BDC1的距离为h
∵VA-BDC1=VC1-ABD=
S△ABD•CC1=
×(
×1×1) ×1=
,
VA-BDC1=VC1-ABD=
S△C1AD•h=
×[
×(
)2]×h=
,
∴h=
,即A到平面BDC1的距离为
.
∴B1C1⊥平面AA1B1B,AB1是AC1在平面AA1B1B上的射影
∴∠C1AB1就是AC1与平面AA1B1B所成的角
在△C1AB1中,tan∠C1AB1=
| 1 | ||
|
| ||
| 2 |
∴直线AC1与平面AA1B1B所成的角的正切值为
| ||
| 2 |
(2)过B作BE⊥AC1,垂足为E,连接ED
∵△ABC1≌△ADC1,
∴∠BAC1=∠DAC1

∵AB=AD,∠BAC1=∠DAC1,AE=AE
∴△ABE≌△ADE,
∴∠AEB=∠AED=
| π |
| 2 |
∴∠AEB是二面角B-AC1-D的平面角
在△DBE中,BE=ED=
| ||
| 3 |
| 2 |
∴cos∠AEB=-
| 1 |
| 2 |
∴二面角B-AC1-D的大小为120°.
(3)设点A到平面BDC1的距离为h
∵VA-BDC1=VC1-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
VA-BDC1=VC1-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 2 |
| ||
| 6 |
∴h=
| ||
| 3 |
| ||
| 3 |
点评:本题是中档题,考查直线与平面所成的角,点、线、面的距离,二面角的应用,考查空间想象能力,计算能力.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 已知正方体ABCD-A1B1C1D1的棱长为a,
已知正方体ABCD-A1B1C1D1的棱长为a, 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1, 如图:已知正方体ABCD-A1B1C1D1中,点F为A1D的中点.
如图:已知正方体ABCD-A1B1C1D1中,点F为A1D的中点. 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.