题目内容
设集合 ,
, ,则
,则 ( )
( )
A.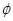 | B.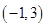 | C.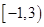 | D.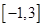 |
C
解析试题分析:因为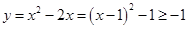 ,所以
,所以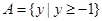 ,即
,即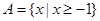 。因为
。因为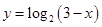 所以
所以 ,所以
,所以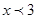 ,即
,即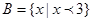 ,所以
,所以 。故C正确。
。故C正确。
考点:一元二次函数的值域,对数的定义域,集合的运算。

练习册系列答案
相关题目
已知集合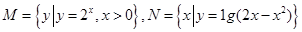 ,则
,则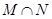 为( )
为( )
| A.(1,2) | B.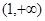 | C.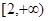 | D.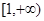 |
已知集合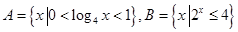 ,则
,则 ( )
( )
A.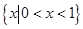 | B.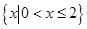 | C.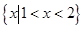 | D.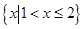 |
已知全集 ,集合
,集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知集合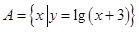 ,
,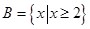 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.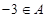 | B.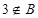 | C.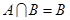 | D. |
已知全集 ,
,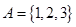 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知集合M={x|y=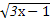 },N={x|y=log2(x-2x2)},则
},N={x|y=log2(x-2x2)},则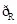 (M∩N)=( )
(M∩N)=( )
A.( , , ) ) | B.(-∞, )∪[ )∪[ ,+∞) ,+∞) |
C.[0, ] ] | D.(-∞,0]∪[ ,+∞) ,+∞) |
已知全集U={y|y=log2x,x>1},集合P=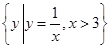 ,则∁UP=( ).
,则∁UP=( ).
A.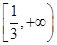 | B.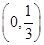 | C.(0,+∞) | D.(-∞,0)∪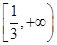 |
设集合A={x|2x≤4},集合B为函数y=lg(x-1)的定义域,则A∩B=( ).
| A.(1,2) | B.[1,2] | C.[1,2) | D.(1,2] |