题目内容
一射击运动员进行飞碟射击训练,每一次射击命中飞碟的概率p与运动员离飞碟的距离s(米)成反比,每一个飞碟飞出后离运动员的距离s(米)与飞行时间t(秒)满足s=15(t+1)(0≤t≤4),每个飞碟允许该运动员射击两次(若第一次射击命中,则不再进行第二次射击).该运动员在每一个飞碟飞出0.5秒时进行第一次射击,命中的概率为 ,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第二次射击,子弹的飞行时间忽略不计.
,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第二次射击,子弹的飞行时间忽略不计.
(1)在第一个飞碟的射击训练时,若该运动员第一次射击没有命中,求他第二次射击命中飞碟的概率;
(2)求第一个飞碟被该运动员命中的概率;
(3)若该运动员进行三个飞碟的射击训练(每个飞碟是否被命中互不影响),求他至少命中两个飞碟的概率.
解:(1)每一次射击命中飞碟的概率p与运动员离飞碟的距离s(米)成反比,
依题意设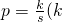 为常数),由于s=15(t+1)(0≤t≤4),
为常数),由于s=15(t+1)(0≤t≤4),
∴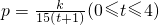 .
.
当t=0.5时,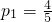 ,则
,则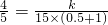 ,解得k=18.
,解得k=18.
∴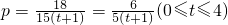 .
.
当t=1时,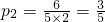 .
.
∴该运动员第二次射击命中飞碟的概率为 .
.
(2)设“该运动员第一次射击命中飞碟”为事件A
第二次命中飞碟为事件B,则“第一个飞碟被该运动员命中”为事件: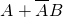 .
.
∵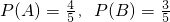 ,
,
∴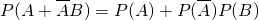 =
=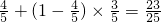 .
.
∴第一个飞碟被该运动员命中的概率为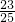 .
.
(3)设该运动员进行三个飞碟的射击训练时命中飞碟的个数为ξ,
由题意知ξ符合独立重复试验,
∴至少命中两个飞碟的概率为P=P(ξ=2)+P(ξ=3)
=C32p2(1-p)+C33p3=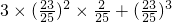 =
=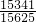 .
.
分析:(1)每一次射击命中飞碟的概率p与运动员离飞碟的距离s(米)成反比,列出关系式,代入s=15(t+1),根据每一个飞碟飞出0.5秒时进行第一次射击,命中的概率为 ,求出系数,得到结果.
,求出系数,得到结果.
(2)第一个飞碟被该运动员命中包括该运动员第一次射击命中飞碟,或是第一次没有命中飞碟且第二次命中飞碟,这两种情况是互斥的,根据相互独立事件的概率和互斥事件的概率公式,得到结果.
(3)该运动员进行三个飞碟的射击训练时命中飞碟的个数为ξ,ξ符合独立重复试验,运动员至少命中两个飞碟包括命中两个飞碟和命中三个飞碟,这两种情况是互斥的,写出概率.
点评:本题考查独立重复试验,考查相互独立事件同时发生的概率,考查互斥事件的概率,考查利用概率知识解决实际问题的能力,是一个概率的综合题目.
依题意设
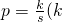 为常数),由于s=15(t+1)(0≤t≤4),
为常数),由于s=15(t+1)(0≤t≤4),∴
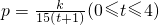 .
.当t=0.5时,
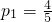 ,则
,则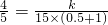 ,解得k=18.
,解得k=18.∴
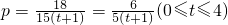 .
.当t=1时,
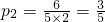 .
.∴该运动员第二次射击命中飞碟的概率为
 .
.(2)设“该运动员第一次射击命中飞碟”为事件A
第二次命中飞碟为事件B,则“第一个飞碟被该运动员命中”为事件:
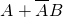 .
.∵
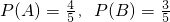 ,
,∴
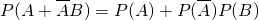 =
=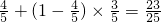 .
.∴第一个飞碟被该运动员命中的概率为
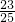 .
.(3)设该运动员进行三个飞碟的射击训练时命中飞碟的个数为ξ,
由题意知ξ符合独立重复试验,
∴至少命中两个飞碟的概率为P=P(ξ=2)+P(ξ=3)
=C32p2(1-p)+C33p3=
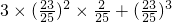 =
=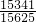 .
.分析:(1)每一次射击命中飞碟的概率p与运动员离飞碟的距离s(米)成反比,列出关系式,代入s=15(t+1),根据每一个飞碟飞出0.5秒时进行第一次射击,命中的概率为
 ,求出系数,得到结果.
,求出系数,得到结果.(2)第一个飞碟被该运动员命中包括该运动员第一次射击命中飞碟,或是第一次没有命中飞碟且第二次命中飞碟,这两种情况是互斥的,根据相互独立事件的概率和互斥事件的概率公式,得到结果.
(3)该运动员进行三个飞碟的射击训练时命中飞碟的个数为ξ,ξ符合独立重复试验,运动员至少命中两个飞碟包括命中两个飞碟和命中三个飞碟,这两种情况是互斥的,写出概率.
点评:本题考查独立重复试验,考查相互独立事件同时发生的概率,考查互斥事件的概率,考查利用概率知识解决实际问题的能力,是一个概率的综合题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
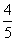 ,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第一次射击,子弹的飞行时间忽略小计.
,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第一次射击,子弹的飞行时间忽略小计. 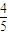 ,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第二次射击,子弹的飞行时间忽略不计.
,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第二次射击,子弹的飞行时间忽略不计.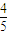 ,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第二次射击,子弹的飞行时间忽略不计.
,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第二次射击,子弹的飞行时间忽略不计.