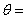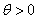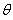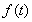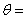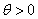题目内容
 随着生活水平的提高,儿童的身高越来越成为人们关注的话题,某心理研究机构从边区某小学四年级学生中随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).
随着生活水平的提高,儿童的身高越来越成为人们关注的话题,某心理研究机构从边区某小学四年级学生中随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).(1)现先用分层抽样的方法从各组中共选取20人作为样本,然后再从第四组或第五组选出的人中选出两人进行进一步分析,则这两人来自不同组的概率是多少?
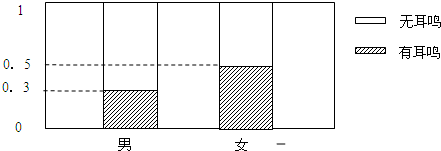
(2)若将身高超过130cm称为正常,低于130cm称为偏低,抽出的20名学生按性别与身高统计具体分布情况如下:
| 男 | 女 | |
| 正常 | 2 | 5 |
| 偏低 | 10 | 3 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
| n(ad-bc)2 |
| (a+c)(b+d)(a+b)(c+d) |
分析:(1)先求出这两组内的同学中抽取的人数,根据所有的选法有
种,这两人身高不在同一组内的选法有2×4种,由此求得两人身高不在同一组内的概率.
(2)根据所给的表格中的数据,代入求观测值的公式,求出观测值同临界值进行比较,得到有95%以上的把握认为学生身高是否正常与性别有关.
| C | 2 6 |
(2)根据所给的表格中的数据,代入求观测值的公式,求出观测值同临界值进行比较,得到有95%以上的把握认为学生身高是否正常与性别有关.
解答:解:(1)由题意知第四组和第五组总人数分别为:
0.02×10×100=20,
0.01×10×100=10.
用分层抽样的方法在第四组内抽取的人数之比为20×
=4,
在第四组内抽取的人数之比为10×
=2,
∴从第四组或第五组选出的人中选出两人共
=15,这两人来自不同组有4×2=8.
∴这两人来自不同组的概率是P=
.
(2)k2=
=4.43>841,
对照参考表格,结合考虑样本是采取分层抽样抽出的,可知有95%以上的把握认为学生身高与性别有关.
0.02×10×100=20,
0.01×10×100=10.
用分层抽样的方法在第四组内抽取的人数之比为20×
| 20 |
| 100 |
在第四组内抽取的人数之比为10×
| 20 |
| 100 |
∴从第四组或第五组选出的人中选出两人共
| C | 2 6 |
∴这两人来自不同组的概率是P=
| 8 |
| 15 |
(2)k2=
| 20×(50-6) 2 |
| 7×13×12×8 |
对照参考表格,结合考虑样本是采取分层抽样抽出的,可知有95%以上的把握认为学生身高与性别有关.
点评:本题主要考查等可能事件的概率,频率分步直方图的应用,独立性检验的应用,本题是一个概率与统计的综合题目,是一个考查的比较全面的解答题.

练习册系列答案
相关题目