题目内容
已知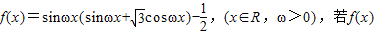 的最小正周期为2π.
的最小正周期为2π.(I)求f(x)的表达式和f(x)的单调递增区间;
(II)求
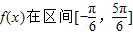 的最大值和最小值.
的最大值和最小值.
【答案】分析:(I)利用两角和与差的正弦将f(x)=sinωx(sinωx+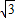 cosωx)-
cosωx)- 化简为f(x)=sin(2ωx-
化简为f(x)=sin(2ωx-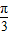 ),由其最小正周期为2π,可求得ω,从而可求f(x)的表达式;由正弦函数的单调性即可求得
),由其最小正周期为2π,可求得ω,从而可求f(x)的表达式;由正弦函数的单调性即可求得
f(x)的单调递增区间;
(II))由-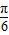 ≤x≤
≤x≤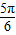 -可求得
-可求得 ≤x-
≤x-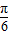 ≤
≤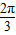 ,由正弦函数的单调性即可求得其最大值和最小值.
,由正弦函数的单调性即可求得其最大值和最小值.
解答:解:(1)∵f(x)=sinωx(sinωx+ cosωx)-
cosωx)-
=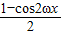 +
+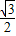 sin2ωx-
sin2ωx-
=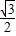 sin2ωx-
sin2ωx- cos2ωx
cos2ωx
=sin(2ωx-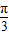 )…3′
)…3′
又f(x)的周期为2π,2π=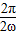 ⇒ω=
⇒ω= ,…4′
,…4′
∴f(x)=sin(x-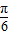 )…5′
)…5′
由2kπ-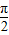 ≤x-
≤x-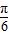 ≤2kπ+
≤2kπ+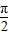 (k∈Z)⇒2kπ-
(k∈Z)⇒2kπ- ≤x≤2kπ+
≤x≤2kπ+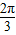 (k∈Z),
(k∈Z),
即f(x)的单调递增区间为[2kπ-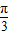 ,2kπ+
,2kπ+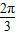 ](k∈Z),…7′
](k∈Z),…7′
(2)∵-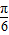 ≤x≤
≤x≤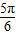 ,
,
∴- ≤x-
≤x-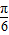 ≤
≤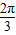 ,…8′
,…8′
∴当x-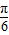 =
=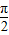 ,即x=
,即x=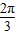 时,f(x)max=1;
时,f(x)max=1;
当x-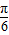 =-
=-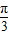 ,即x=-
,即x=-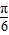 时,f(x)min=-
时,f(x)min=-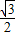 ,…12′
,…12′
∴当x=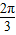 时,f(x)max=1;当x=-
时,f(x)max=1;当x=-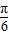 时,f(x)min=-
时,f(x)min=-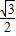 …13
…13
点评:本题考查两角和与差的正弦,考查正弦函数的单调性、周期性与最值,求得f(x)的解析式是关键,属于中档题.
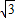 cosωx)-
cosωx)- 化简为f(x)=sin(2ωx-
化简为f(x)=sin(2ωx-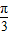 ),由其最小正周期为2π,可求得ω,从而可求f(x)的表达式;由正弦函数的单调性即可求得
),由其最小正周期为2π,可求得ω,从而可求f(x)的表达式;由正弦函数的单调性即可求得f(x)的单调递增区间;
(II))由-
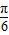 ≤x≤
≤x≤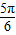 -可求得
-可求得 ≤x-
≤x-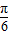 ≤
≤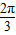 ,由正弦函数的单调性即可求得其最大值和最小值.
,由正弦函数的单调性即可求得其最大值和最小值.解答:解:(1)∵f(x)=sinωx(sinωx+
 cosωx)-
cosωx)-
=
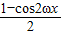 +
+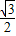 sin2ωx-
sin2ωx-
=
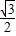 sin2ωx-
sin2ωx- cos2ωx
cos2ωx=sin(2ωx-
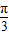 )…3′
)…3′又f(x)的周期为2π,2π=
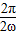 ⇒ω=
⇒ω= ,…4′
,…4′∴f(x)=sin(x-
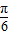 )…5′
)…5′由2kπ-
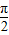 ≤x-
≤x-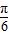 ≤2kπ+
≤2kπ+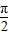 (k∈Z)⇒2kπ-
(k∈Z)⇒2kπ- ≤x≤2kπ+
≤x≤2kπ+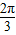 (k∈Z),
(k∈Z),即f(x)的单调递增区间为[2kπ-
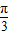 ,2kπ+
,2kπ+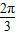 ](k∈Z),…7′
](k∈Z),…7′(2)∵-
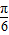 ≤x≤
≤x≤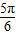 ,
,∴-
 ≤x-
≤x-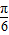 ≤
≤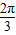 ,…8′
,…8′∴当x-
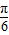 =
=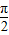 ,即x=
,即x=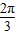 时,f(x)max=1;
时,f(x)max=1;当x-
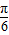 =-
=-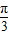 ,即x=-
,即x=-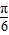 时,f(x)min=-
时,f(x)min=-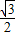 ,…12′
,…12′∴当x=
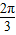 时,f(x)max=1;当x=-
时,f(x)max=1;当x=-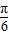 时,f(x)min=-
时,f(x)min=-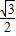 …13
…13点评:本题考查两角和与差的正弦,考查正弦函数的单调性、周期性与最值,求得f(x)的解析式是关键,属于中档题.

练习册系列答案
相关题目
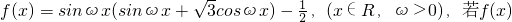 的最小正周期为2π.
的最小正周期为2π. 的最大值和最小值.
的最大值和最小值.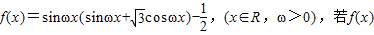 的最小正周期为2π.
的最小正周期为2π.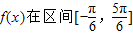 的最大值和最小值.
的最大值和最小值.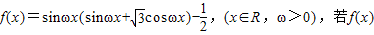 的最小正周期为2π.
的最小正周期为2π.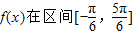 的最大值和最小值.
的最大值和最小值.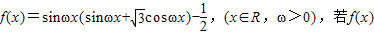 的最小正周期为2π.
的最小正周期为2π.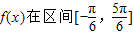 的最大值和最小值.
的最大值和最小值.