题目内容
先后随机投掷2枚质地均匀正方体骰子(2枚骰子每个面分别标有1,2,3,4,5,6),其中x表示第1枚骰子出现的点数,y表示第2枚骰子出现的点数.设点P的坐标为(x,y).(1)求点P(x,y)在直线y=x-1上的概率
(2)求点P(x.y)满足y2<4x的概率.
【答案】分析:(1)先求出先后随机投掷2枚质地均匀正方体骰子,点P的坐标可能出现的情况,为36种,再找出点P(x,y)在直线y=x-1上的情况,除以36即可.
(2)按x=1,2,3,4,5,6一一列举出P(x.y)满足y2<4x的概率的情况.=,再除以36即可.
解答:解:(1)先后随机投掷2枚质地均匀正方体骰 子,第1枚骰子出现的点数x可以是1,2,3,4,5,6,
第2枚骰子出现的点数y可以是1,2,3,4,5,6∴点P的可能情况有6×6=36种.
点P(x,y)在直线y=x-1上的情况,有5种,(2,1),(3,2),(4,3),(5,4),(6,5)
∴点P(x,y)在直线y=x-1上的概率为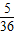 .
.
(2)若点P(x.y)满足y2<4x,则点P(x.y)在抛物线y2=4x内部
把x=1代入抛物线y2=4x,得,y=2,∴P点坐标为(1,1)时满足y2<4x
把x=2代入抛物线y2=4x,得y=2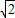 ≈2.828,∴P点坐标为(2,1),(2,2)时满足y2<4x
≈2.828,∴P点坐标为(2,1),(2,2)时满足y2<4x
把x=3代入抛物线y2=4x,得y=2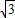 ≈3.464,∴P点坐标为(3,1),(3,2),(3,3)时满足y2<4x
≈3.464,∴P点坐标为(3,1),(3,2),(3,3)时满足y2<4x
把x=4代入抛物线y2=4x,得y=4,∴P点坐标为(4,1),(4,2),(4,3)时满足y2<4x
把x=5代入抛物线y2=4x,得y=2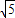 ≈4.472,,∴P点坐标为(5,1),(5,2),(5,3),(5,4)时满足y2<4x
≈4.472,,∴P点坐标为(5,1),(5,2),(5,3),(5,4)时满足y2<4x
把x=6代入抛物线y2=4x,得y=2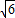 ≈4.898,,∴P点坐标为(6,1),(6,2),(6,3),(6,4)时满足y2<4x
≈4.898,,∴P点坐标为(6,1),(6,2),(6,3),(6,4)时满足y2<4x
∴满足y2<4x的点共有1+2+3+3+4+4=17种
点P(x.y)满足y2<4x的概率=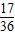 .
.
点评:本题考查了等可能性事件概率的求法,做题时不要丢情况.
(2)按x=1,2,3,4,5,6一一列举出P(x.y)满足y2<4x的概率的情况.=,再除以36即可.
解答:解:(1)先后随机投掷2枚质地均匀正方体骰 子,第1枚骰子出现的点数x可以是1,2,3,4,5,6,
第2枚骰子出现的点数y可以是1,2,3,4,5,6∴点P的可能情况有6×6=36种.
点P(x,y)在直线y=x-1上的情况,有5种,(2,1),(3,2),(4,3),(5,4),(6,5)
∴点P(x,y)在直线y=x-1上的概率为
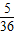 .
.(2)若点P(x.y)满足y2<4x,则点P(x.y)在抛物线y2=4x内部
把x=1代入抛物线y2=4x,得,y=2,∴P点坐标为(1,1)时满足y2<4x
把x=2代入抛物线y2=4x,得y=2
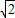 ≈2.828,∴P点坐标为(2,1),(2,2)时满足y2<4x
≈2.828,∴P点坐标为(2,1),(2,2)时满足y2<4x把x=3代入抛物线y2=4x,得y=2
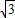 ≈3.464,∴P点坐标为(3,1),(3,2),(3,3)时满足y2<4x
≈3.464,∴P点坐标为(3,1),(3,2),(3,3)时满足y2<4x把x=4代入抛物线y2=4x,得y=4,∴P点坐标为(4,1),(4,2),(4,3)时满足y2<4x
把x=5代入抛物线y2=4x,得y=2
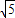 ≈4.472,,∴P点坐标为(5,1),(5,2),(5,3),(5,4)时满足y2<4x
≈4.472,,∴P点坐标为(5,1),(5,2),(5,3),(5,4)时满足y2<4x把x=6代入抛物线y2=4x,得y=2
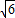 ≈4.898,,∴P点坐标为(6,1),(6,2),(6,3),(6,4)时满足y2<4x
≈4.898,,∴P点坐标为(6,1),(6,2),(6,3),(6,4)时满足y2<4x∴满足y2<4x的点共有1+2+3+3+4+4=17种
点P(x.y)满足y2<4x的概率=
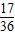 .
.点评:本题考查了等可能性事件概率的求法,做题时不要丢情况.

练习册系列答案
相关题目