题目内容
设双曲线C:
=1的左、右焦点分别为F1、F2，点P是双曲线位于第一象限内的一个点，且满足
·
=0,则△PF1F2的内切圆的方程为A.(x-2)2+(y-1)2=1 B.(x-3)2+(y-2)2=4
C.(x-3)2+(y-1)2=1 D.(x-4)2+(y-2)2=4
B 由题意：双曲线的左、右焦点F1（-5,0)、F2(5,0),如示意图所示.
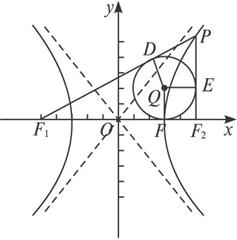
设P(x0,y0),则x0=5,y0=,∴P(5,).
设内切圆圆心为Q,切点分别为D、E、F,
则|PF1|-|PF2|=|DF1|-|EF2|=|F1F|-|FF2|=6,①
又|F1F|+|FF2|=10,②
由①②,得|F1F|=8，|FF2|=2，∴|OF|=3.
故内切圆表示以Q(3,2)为圆心,2为半径的圆,
故△PF1F2的内切圆方程为(x-3)2+(y-2)2=4.
练习册系列答案
相关题目
的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q。
，求点T的坐标；
，若
（T为（Ⅰ）中的点）的取值范围。
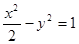的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点
。
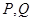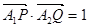，求点T的坐标；
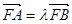，若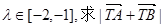
（T为（1）中的点）的取值范围。
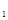,F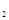
分别是双曲线C：
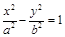的左．右焦点，过F
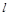与双曲线的左支相交于A\B两点，且
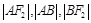成等差数列，则双曲线的离心率为
．
=1的左、右焦点，若点P在双曲线上，且
·
=0，则|
+
|等于( )
B.2
C.
D.2