题目内容
若函数f(x)在其定义域内某一区间[a,b]上连续,且对[a,b]中任意实数x1,x2,都有f(
)≤
,则称函数f(x)在[a,b]上是下凸函数;有以下几个函数:
①f(x)=x2+ax+b,x∈R;
②f(x)=x+
,x∈(0,+∞);
③f(x)=sinx,x∈[0,2π);
④f(x)=tanx,x∈(-
,
);
⑤f(x)=log
x,x∈(0,+∞).
其中是下凸函数的是
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
①f(x)=x2+ax+b,x∈R;
②f(x)=x+
| 1 |
| x |
③f(x)=sinx,x∈[0,2π);
④f(x)=tanx,x∈(-
| π |
| 2 |
| π |
| 2 |
⑤f(x)=log
| 1 |
| 2 |
其中是下凸函数的是
①②⑤
①②⑤
.分析:由已知中下凸函数的定义,我们可以判断出下凸函数的图象形状,根据二次函数,对勾函数,正弦函数,正切函数,对数函数的图象和性质,逐一比照后可得答案.
解答:解:由已知中下凸函数的定义,可得下凸函数的图象形状可能为:
 或
或 或
或
可得函数f(x)=x2+ax+b,x∈R为下凸函数
函数f(x)=x+
,x∈(0,+∞)为下凸函数
函数f(x)=sinx,x∈[π,2π)为下凸函数,函数f(x)=sinx,x∈[0,2π)不为下凸函数;
函数f(x)=tanx,x∈(0,
)为下凸函数,函数f(x)=tanx,x∈(-
,
)不为下凸函数
函数f(x)=log
x,x∈(0,+∞)为下凸函数
故答案为:①②⑤
 或
或 或
或
可得函数f(x)=x2+ax+b,x∈R为下凸函数
函数f(x)=x+
| 1 |
| x |
函数f(x)=sinx,x∈[π,2π)为下凸函数,函数f(x)=sinx,x∈[0,2π)不为下凸函数;
函数f(x)=tanx,x∈(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
函数f(x)=log
| 1 |
| 2 |
故答案为:①②⑤
点评:本题考查的知识点是正切函数的图象,二次函数的图象,对数函数的图象,正弦函数的图象,其中根据下凸函数的定义判断出下凸函数的图象形状是解答本题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
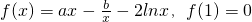 .
.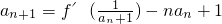 .
.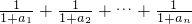 与
与 的大小,并说明你的理由.
的大小,并说明你的理由. .
. .
. 与
与 的大小,并说明你的理由.
的大小,并说明你的理由. -2lnx,f(1)=0,
-2lnx,f(1)=0, -nan+1,
-nan+1, 的大小,并说明你的理由。
的大小,并说明你的理由。  .
. .
. 与
与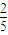 的大小,并说明你的理由.
的大小,并说明你的理由.