题目内容
为了判断高中学生选读文科是否与性别有关,现随机抽取50名学生,得到如下2×2列联表:
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025,根据表中数据,得到K2=
≈4.844,则在犯错误的概率不超过
| 理科 | 文科 | 合计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
| 50×(13×20-10×7)2 |
| 23×27×20×30 |
5%
5%
的前提下可以认为选读文科与性别是有关系的.分析:根据条件中所给的观测值,同所给的临界值进行比较,根据4.844>3.841,即可得到认为选修文科与性别有关系出错的可能性为5%.
解答:解:∵根据表中数据,得到K2的观测值解K2=
≈4.844,
因为4.844>3.841,
∴认为选修文科与性别有关系出错的可能性为5%.
故答案为:5%.
| 50×(13×20-10×7)2 |
| 23×27×20×30 |
因为4.844>3.841,
∴认为选修文科与性别有关系出错的可能性为5%.
故答案为:5%.
点评:本题考查独立性检验的应用,本题解题的关键是正确理解观测值对应的概率的意义.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
为了判断高中学生选读文科是否与性别有关,现随机抽取50名学生,得到如下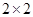 列联表:
列联表:
|
|
理科 |
文科 |
合计 |
|
男 |
13 |
10 |
23 |
|
女 |
7 |
20 |
27 |
|
合计 |
20 |
30 |
50 |
已知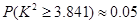 ,
,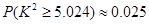 ,根据表中数据,得到
,根据表中数据,得到
 ,则在犯错误的概率不超过
的前提下可以认为选读文科与性别是有关系的。
,则在犯错误的概率不超过
的前提下可以认为选读文科与性别是有关系的。
为了判断高中学生选读文科是否与性别有关,现随机抽取50名学生,得到如下2×2列联表:
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025,根据表中数据,得到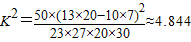 ,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的.
,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的.
| 理科 | 文科 | 合计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
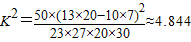 ,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的.
,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的.