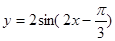题目内容
设函数 .
.
(1)求 的最小正周期。
的最小正周期。
(2)若函数 与
与 的图像关于直线
的图像关于直线 对称,求当
对称,求当 时
时 的最大值.
的最大值.
 .
.(1)求
 的最小正周期。
的最小正周期。(2)若函数
 与
与 的图像关于直线
的图像关于直线 对称,求当
对称,求当 时
时 的最大值.
的最大值.(1)8.(2)

试题分析:(1)先将三角函数化为基本三角函数,即利用降幂公式及两角差正弦公式得:
 =
=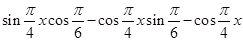 =
= =
=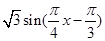 ,再利用基本三角函数性质得:T =
,再利用基本三角函数性质得:T = 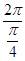 =8.(2)利用转移法,先求出
=8.(2)利用转移法,先求出 解析式. 在
解析式. 在 的图象上任取一点
的图象上任取一点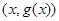 ,它关于
,它关于 的对称点
的对称点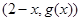 在
在 的图象上,从而
的图象上,从而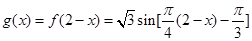 =
=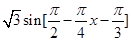 =
= , 当
, 当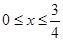 时,
时,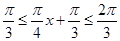 ,因此
,因此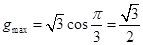 .
.试题解析:(1)
 =
=
=
 =
=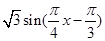
故
 的最小正周期为T =
的最小正周期为T = 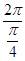 =8.
=8.(2)在
 的图象上任取一点
的图象上任取一点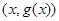 ,它关于
,它关于 的对称点
的对称点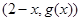 .
.由题设条件,点
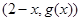 在
在 的图象上,从而
的图象上,从而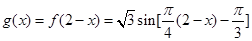 =
=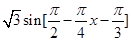 =
=
当
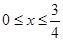 时,
时,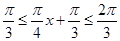 ,因此
,因此 在区间
在区间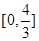 上的最大值为
上的最大值为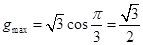

练习册系列答案
相关题目
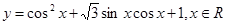 .
.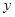 取得最大值时,求自变量
取得最大值时,求自变量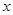 的集合;
的集合;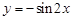 ;②
;②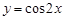 ;③
;③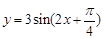 ,其图象仅通过向左(或向右)平移就能与函数
,其图象仅通过向左(或向右)平移就能与函数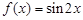 的图象重合的是_____.(填上符合要求的函数对应的序号)
的图象重合的是_____.(填上符合要求的函数对应的序号) 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( ) 个单位长度
个单位长度 个单位长度
个单位长度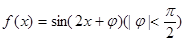 的图象向左平移
的图象向左平移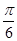 个单位后关于原点对称,则函
个单位后关于原点对称,则函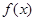 在
在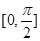 上的最小值为( )
上的最小值为( )



 的部分图像如图所示,则
的部分图像如图所示,则 和
和 的值可以是( )
的值可以是( )




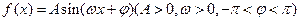 的部分图象如图所示,则函数
的部分图象如图所示,则函数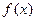 的解析式为( )
的解析式为( )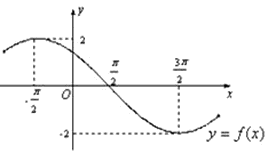




 ,则方程
,则方程 的解是_____________.
的解是_____________.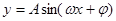 在一个周期内的图象如右,此函数的解析式为( )
在一个周期内的图象如右,此函数的解析式为( )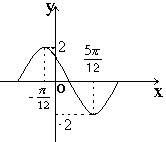
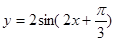 B.
B.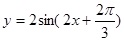
 D.
D.