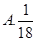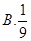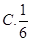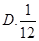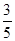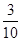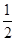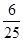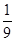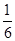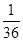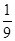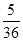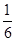题目内容
某车间共有6名工人,他们某日加工零件个数的茎叶图如上图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为( ) 
A. | B.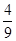 | C. | D.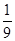 |
A
解析试题分析:解:
因为六名工人的日加工零件个数互不相同,可用该数据代表相应的工人,则从他们中任取两人,共有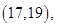
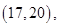
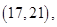
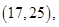
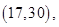
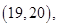
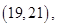
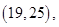
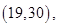
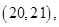

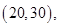

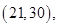
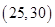 15个基本结果,由于是任取的,所以每个结果出现的可能性是相等的,其中恰有一名优秀工人的有
15个基本结果,由于是任取的,所以每个结果出现的可能性是相等的,其中恰有一名优秀工人的有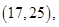
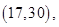
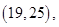
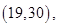

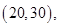

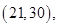 共8个,所以恰有一名优秀工人的概率为
共8个,所以恰有一名优秀工人的概率为 ,故选A.
,故选A.
考点:古典概型;2、茎叶图;3、均值的概念.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知实数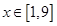 ,执行如下图所示的程序框图,则输出的x不小于55的概率为( )
,执行如下图所示的程序框图,则输出的x不小于55的概率为( )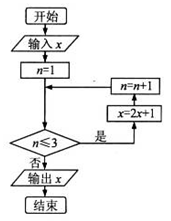
A.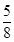 | B.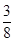 | C.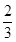 | D.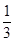 |
设随机变量X~N(2,32),若P(X≤c)=P(X>c),则c等于( )
| A.0 | B.1 | C.2 | D.3 |
在区间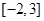 上随机选取一个数
上随机选取一个数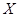 ,则
,则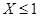 的概率为( )
的概率为( )
A.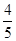 | B.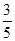 | C.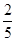 | D.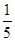 |
[2014·抚顺模拟]已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,则P(-2≤ξ≤2)=( )
| A.0.477 | B.0.628 | C.0.954 | D.0.977 |