题目内容
函数

| A.是偶函数 | B.是奇函数 |
| C.既是偶函数又是奇函数 | D.既不是偶函数也不是奇函数 |
A
析:根据题意可得函数的定义域关于原点对称,然后对函数进行化简,而函数满足f(-x)=cos(-x)=cosx=f(x),所以可以判断函数是偶函数.
解答:解:由题意可得:函数的定义域关于原点对称,
又因为函数 ,
,
所以f(x)=y=cosx,x∈R,
所以f(-x)=cos(-x)=cosx=f(x),
所以函数f(x)=cosx是偶函数,
所以函数 是偶函数.
是偶函数.
故选A.
解答:解:由题意可得:函数的定义域关于原点对称,
又因为函数
 ,
,所以f(x)=y=cosx,x∈R,
所以f(-x)=cos(-x)=cosx=f(x),
所以函数f(x)=cosx是偶函数,
所以函数
 是偶函数.
是偶函数.故选A.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
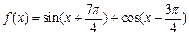 ,x
,x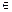 R.
R. 的最小正周期和最小值;
的最小正周期和最小值;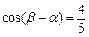 ,
,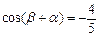 ,
,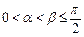 .求证:
.求证: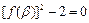 .
.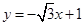 的倾斜角为( ※ )
的倾斜角为( ※ )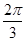



 满足
满足 ,
, ,则
,则 等于
等于



 ,且
,且 为第四象限的角,求
为第四象限的角,求 ,
, 的值。
的值。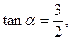 则
则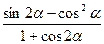 =_____________ .
=_____________ .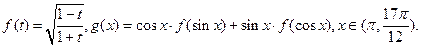 ,化简g(x)
,化简g(x)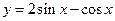 的最大值为 。
的最大值为 。 是方程
是方程 (
( 为常数) 的两个根.
为常数) 的两个根. ;
;