题目内容
三个女生和五个男生排成一排.
(1)如果女生必须全排在一起,有多少种不同的排法?
(2)如果女生必须全分开,有多少种不同的排法?
(3)如果两端都不能排女生,有多少种不同的排法?
(4)如果两端不能都排女生,有多少种不同的排法?
(1) 4320;(2) 14400;(3) 14400;(4) 36000;
解析试题分析:解:(1)女生全部排在一起有A66A33=4320种.
(2)女生必须全分开有A55A63=14400种.
(3)因为两端都不能排女生,所以两端只能从5个男生中选2个排在两端,有A52种排法,其余6人有A66种排法,
所以共有A52•A66=14400种排法.
(4)8个人站成一排共有P88种不同的排法,排除掉两端都是女生的排法有A25•A66种,
所以符合条件的排法有A88-A32•A66=36000种.
考点:排列组合计数问题
点评:主要是考查了排列组合以及计数问题,在做该试题时,要仔细分析题目的条件,属于中档题。

练习册系列答案
相关题目
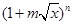 (
( 是正实数)的展开式的二项式系数之和为256,展开式中含
是正实数)的展开式的二项式系数之和为256,展开式中含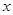 项的系数为112.
项的系数为112.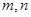 的值;
的值;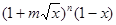 的展开式中含
的展开式中含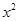 项的系数.
项的系数. ,其中
,其中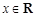 ,
, 为正整数,且
为正整数,且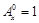 ,这是排列数
,这是排列数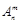 (
( 是正整数,且
是正整数,且 )的一种推广.
)的一种推广.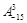 的值;
的值;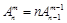 ,②
,②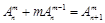 (其中
(其中 是正整数).是否都能推广到
是正整数).是否都能推广到 (
(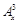 的单调区间.
的单调区间.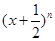 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.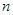 的值;(2)设
的值;(2)设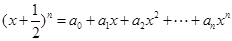 .
.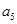 的值; ②求
的值; ②求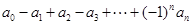 的值.
的值. 展开式中的二项式系数的和比
展开式中的二项式系数的和比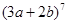 展开式的二项式系数的和大
展开式的二项式系数的和大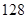 ,求
,求