题目内容
已知向量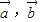 满足
满足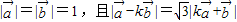 ,其中k>0,
,其中k>0,(1)试用k表示
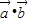 ,并求出
,并求出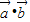 的最大值及此时
的最大值及此时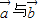 的夹角为θ的值;
的夹角为θ的值;(2)当
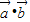 取得最大值时,求实数λ,使
取得最大值时,求实数λ,使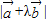 的值最小,并对这一结果作出几何解释.
的值最小,并对这一结果作出几何解释.
【答案】分析:(1)由已知可得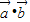 =-(
=-( 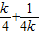 ),利用基本不等式可得
),利用基本不等式可得 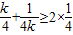 =
= ,故
,故 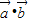 ≤-
≤- ,此时,
,此时,
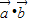 =-
=- =1×1cosθ,θ=120°.
=1×1cosθ,θ=120°.
(2)当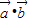 取得最大值时,
取得最大值时,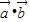 =-
=- =
=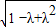 ,故当λ=
,故当λ= 时,
时,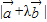 的最小值等于
的最小值等于 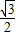 ,
,
这一结果的几何解释:平行四边形OABC中,OA=1,∠AOC=120°,当且仅当OC= 时,对角线OB最短为
时,对角线OB最短为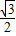 .
.
解答:解:(1)∵|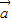 |=|
|=| |=1,
|=1,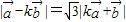 ,
,
∴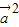 -2k
-2k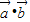 +
+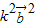 =3k2
=3k2 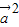 +6k
+6k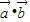 +3
+3 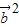 ,∴1-2k
,∴1-2k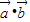 +k2=3k2+6k
+k2=3k2+6k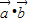 +3,
+3,
∴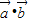 =-(
=-( 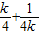 ).∵
).∵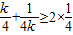 =
= ,
,
∴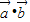 ≤-
≤- ,当且仅当
,当且仅当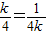 ,即k=1时,取等号.
,即k=1时,取等号.
此时,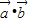 =-
=- =1×1cosθ,∴θ=120°.
=1×1cosθ,∴θ=120°.
(2)当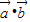 取得最大值时,
取得最大值时,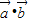 =-
=- ,
,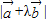 =
=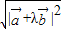 =
=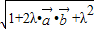 =
=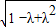 ,
,
故当λ= 时,
时,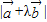 的最小值等于
的最小值等于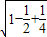 =
=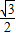 ,
,
这一结果的几何解释:平行四边形OABC中,OA=1,∠AOC=120°,当且仅当OC= 时,对角线OB最短为
时,对角线OB最短为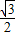 .
.
点评:本题考查两个向量的数量积公式,两个向量的数量积的定义,求向量的模的方法,基本不等式的应用,是一道中档题.
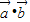 =-(
=-( 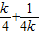 ),利用基本不等式可得
),利用基本不等式可得 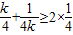 =
= ,故
,故 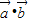 ≤-
≤- ,此时,
,此时,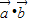 =-
=- =1×1cosθ,θ=120°.
=1×1cosθ,θ=120°.(2)当
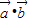 取得最大值时,
取得最大值时,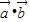 =-
=- =
=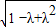 ,故当λ=
,故当λ= 时,
时,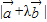 的最小值等于
的最小值等于 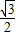 ,
,这一结果的几何解释:平行四边形OABC中,OA=1,∠AOC=120°,当且仅当OC=
 时,对角线OB最短为
时,对角线OB最短为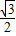 .
.解答:解:(1)∵|
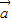 |=|
|=| |=1,
|=1,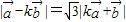 ,
,∴
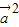 -2k
-2k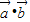 +
+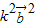 =3k2
=3k2 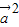 +6k
+6k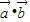 +3
+3 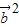 ,∴1-2k
,∴1-2k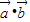 +k2=3k2+6k
+k2=3k2+6k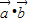 +3,
+3,∴
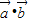 =-(
=-( 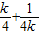 ).∵
).∵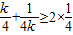 =
= ,
,∴
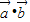 ≤-
≤- ,当且仅当
,当且仅当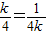 ,即k=1时,取等号.
,即k=1时,取等号.此时,
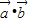 =-
=- =1×1cosθ,∴θ=120°.
=1×1cosθ,∴θ=120°.(2)当
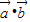 取得最大值时,
取得最大值时,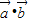 =-
=- ,
,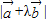 =
=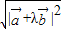 =
=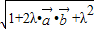 =
=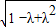 ,
,故当λ=
 时,
时,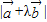 的最小值等于
的最小值等于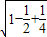 =
=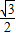 ,
,这一结果的几何解释:平行四边形OABC中,OA=1,∠AOC=120°,当且仅当OC=
 时,对角线OB最短为
时,对角线OB最短为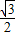 .
.点评:本题考查两个向量的数量积公式,两个向量的数量积的定义,求向量的模的方法,基本不等式的应用,是一道中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 满足
满足 ,其中k>0,记函数f(
,其中k>0,记函数f( )=
)= ,
, ,当f(
,当f( 垂直的向量可以是
垂直的向量可以是  B.
B. C.
C. D.
D.
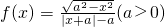 ,既不是奇函数,又不是偶函数;
,既不是奇函数,又不是偶函数;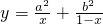 的最小值是a2+b2;
的最小值是a2+b2;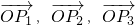 满足条件
满足条件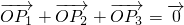 ,且
,且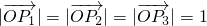 ,则△P1P2P3为正三角形;
,则△P1P2P3为正三角形;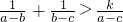 恒成立,则k∈(0,2);
恒成立,则k∈(0,2); 满足
满足 ,其中k>0,
,其中k>0,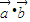 ,并求出
,并求出 的最大值及此时
的最大值及此时 的夹角为θ的值;
的夹角为θ的值; 取得最大值时,求实数λ,使
取得最大值时,求实数λ,使 的值最小,并对这一结果作出几何解释.
的值最小,并对这一结果作出几何解释. ,既不是奇函数,又不是偶函数;
,既不是奇函数,又不是偶函数; 的最小值是a2+b2;
的最小值是a2+b2; 满足条件
满足条件 ,且
,且 ,则△P1P2P3为正三角形;
,则△P1P2P3为正三角形; 恒成立,则k∈(0,2);
恒成立,则k∈(0,2);