题目内容
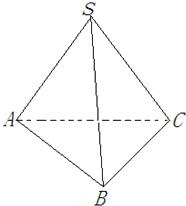如图，已知SA=AB=BC=1，以SC为斜边的Rt△SAC≌Rt△SBC，
．
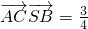（1）求二面角A-SB-C的大小．
（2）求异面直线AS，BC所成角．
解：（1）取M为SB的中点，连接AM，
则AM⊥SB，
∴
∴
．
设二面角A-SB-C为α，∵
，
，
∴AC2=AM2+BC2+BM2-2AM•BC•cosα，
∴
．
（2）
∴
∴异面直线AS，BC所成角为
分析：（1）取M为SB的中点，连接AM，则AM⊥SB，又BC⊥SB，故利用向量
的夹角，利用余弦定理可求二面角A-SB-C的平面角；
（2）异面直线AS，BC所成角转化为向量
的夹角问题，从而得解．
点评：本题以向量为载体，考查面面角，线线角，关键是利用好向量条件．
则AM⊥SB，
∴
∴
．设二面角A-SB-C为α，∵
，，∴AC2=AM2+BC2+BM2-2AM•BC•cosα，
∴
．（2）
∴
∴异面直线AS，BC所成角为
分析：（1）取M为SB的中点，连接AM，则AM⊥SB，又BC⊥SB，故利用向量
的夹角，利用余弦定理可求二面角A-SB-C的平面角；（2）异面直线AS，BC所成角转化为向量
的夹角问题，从而得解．点评：本题以向量为载体，考查面面角，线线角，关键是利用好向量条件．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
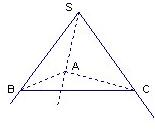如图，已知SA，SB，SC是由一点S引出的不共面的三条射线，∠ASC=∠ASB=45°，∠BSC=60°，∠SAB=90°，求证：AB⊥SC．
如图，已知SA=AB=BC=1，以SC为斜边的Rt△SAC≌Rt△SBC，
．
