题目内容
3.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{4}$=1(a>2)的离心率为$\frac{\sqrt{3}}{3}$,斜率为k的直线l过点E(0,1)且与椭圆交于C,D两点.(1)求椭圆的方程;
(2)若直线l与x轴相交于点G,且$\overrightarrow{GC}$=$\overrightarrow{DE}$,求k的值;
(3)设点A为椭圆的下顶点,kAC,kAD分别为直线AC,AD的斜率,证明:对任意的k,恒有kAC•kAD=-2.
分析 (1)由椭圆的离心率结合隐含条件求得a,c的值,则椭圆方程可求;
(2)由题意设出直线方程,和椭圆方程联立,化为关于x的一元二次方程后利用根与系数的关系可得C,D两点的横坐标的和与积,把$\overrightarrow{GC}$=$\overrightarrow{DE}$转化为点的横坐标间的关系,代入根与系数的关系后求得k值;
(3)由椭圆方程求出A的坐标,得到kAC,kAD,代入根与系数的关系证得答案.
解答 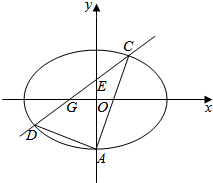 (1)解:由$e=\frac{c}{a}=\frac{\sqrt{3}}{3}$,得$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{3}$,即a2=3c2,
(1)解:由$e=\frac{c}{a}=\frac{\sqrt{3}}{3}$,得$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{3}$,即a2=3c2,
又b2=4,a2=b2+c2,
∴c2=2,a2=6.
则椭圆的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{4}=1$;
(2)解:如图,由题意可知,直线l的斜率存在且不为0,
设其方程为y=kx+1,
联立$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(2+3k2)x2+6kx-9=0.
再设C(x1,y1),D(x2,y2),
则${x}_{1}+{x}_{2}=-\frac{6k}{2+3{k}^{2}},{x}_{1}{x}_{2}=-\frac{9}{2+3{k}^{2}}$,
若$\overrightarrow{GC}$=$\overrightarrow{DE}$,则x1=xG-x2,即x1+x2=xG,
由y=kx+1,取y=0可得${x}_{G}=-\frac{1}{k}$,
∴$-\frac{6k}{2+3{k}^{2}}=-\frac{1}{k}$,解得:$k=±\frac{\sqrt{6}}{3}$;
(3)证明:由题意方程可得A(0,-2),
则${k}_{AC}=\frac{{y}_{1}+2}{{x}_{1}},{k}_{AD}=\frac{{y}_{2}+2}{{x}_{2}}$,
∴kAC•kAD=$\frac{{y}_{1}+2}{{x}_{1}}•\frac{{y}_{2}+2}{{x}_{2}}$=$\frac{{y}_{1}{y}_{2}+2({y}_{1}+{y}_{2})+4}{{x}_{1}{x}_{2}}$.
y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1=${k}^{2}(-\frac{9}{2+3{k}^{2}})+k(-\frac{6k}{2+3{k}^{2}})+1$=$\frac{2-12{k}^{2}}{2+3{k}^{2}}$,
${y}_{1}+{y}_{2}=k({x}_{1}+{x}_{2})+2=k(-\frac{6k}{2+3{k}^{2}})+2$=$\frac{4}{2+3{k}^{2}}$.
∴kAC•kAD=$\frac{\frac{2-12{k}^{2}}{2+3{k}^{2}}+\frac{8}{2+3{k}^{2}}+4}{-\frac{9}{2+3{k}^{2}}}$=$\frac{\frac{18}{2+3{k}^{2}}}{-\frac{9}{2+3{k}^{2}}}=-2$.
点评 本题考查椭圆方程的求法,考查直线和圆锥曲线位置关系的应用,涉及直线与圆锥曲线的关系问题,常采用联立直线方程与圆锥曲线方程,利用一元二次方程的根与系数的关系求解,属中档题.

| A. | 20 | B. | 2$\sqrt{5}$ | C. | $\sqrt{5}$ | D. | 10 |