题目内容
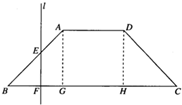
 如图,已知底角为45°的等腰梯形ABCD,底边BC长为5,腰长为2
如图,已知底角为45°的等腰梯形ABCD,底边BC长为5,腰长为2| 2 |
(1)试写出左边部分的面积y与x的函数解析式;
(2)当3≤x<4时,求面积y的取值范围.
分析:(1)直线l把梯形分成两部分,从左向右移动,左边部分是三角形,然后是三角形+矩形,最后是梯形-三角形,从而可得左边部分的面积y与x的函数解析式;
(2)函数y在区间[3,4)随着自变量x的增大而增大,从而可求面积y的取值范围.
(2)函数y在区间[3,4)随着自变量x的增大而增大,从而可求面积y的取值范围.
解答:解:(1)依题意,底角为45°的等腰梯形ABCD,底边BC长为5,腰长为2
,则BG=2,GH=1,BC=5
所以y=
------(7分)
(2)函数y在区间[3,4)随着自变量x的增大而增大,故当x=3时函数取得最小值4,当x=4时,函数取得最大值
,所以当3≤x<4时,面积y的取值范围为[4,
]--------( 10分)
| 2 |
所以y=
|
(2)函数y在区间[3,4)随着自变量x的增大而增大,故当x=3时函数取得最小值4,当x=4时,函数取得最大值
| 11 |
| 2 |
| 11 |
| 2 |
点评:本题考查图形面积的计算,考查面积的最值,考查学生的计算能力,属于中档题.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为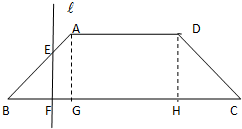 如图,已知底角为45°角的等腰梯形ABCD,底边BC长为7cm,腰长为2
如图,已知底角为45°角的等腰梯形ABCD,底边BC长为7cm,腰长为2
 ,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数.
,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数.