题目内容
请考生从以下三个小题中任选一个作答,若多选,则按所选的第一题计分.
(1)若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为
(2)直线3x-4y-1=0被曲线
(θ为参数)所截得的弦长为
(3)若直角△ABC的内切圆与斜边AB相切于点D,且AD=1,BD=2,则△ABC的面积为
(1)若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为
(0,
)
| 1 |
| 3 |
(0,
)
.| 1 |
| 3 |
(2)直线3x-4y-1=0被曲线
|
2
| 3 |
2
.| 3 |
(3)若直角△ABC的内切圆与斜边AB相切于点D,且AD=1,BD=2,则△ABC的面积为
2
2
.分析:(1)由于|x-1|+|x-m|最小值为|m-1|,则由题意可得0<2m≤|m-1|,解此绝对值不等式求出解集.
(2)把圆的参数方程化为普通方程,求出圆心到直线3x-4y-1=0的距离为d,根据弦长为2
求得结果.
(3)设内切圆半径为r,由勾股定理可得(1+r)2+(2+r)2=9,可得r2+3r=2,再根据△ABC的面积为
×(1+r)(2+r),运算求得结果.
(2)把圆的参数方程化为普通方程,求出圆心到直线3x-4y-1=0的距离为d,根据弦长为2
| r2-d2 |
(3)设内切圆半径为r,由勾股定理可得(1+r)2+(2+r)2=9,可得r2+3r=2,再根据△ABC的面积为
| 1 |
| 2 |
解答:解:(1)由于|x-1|+|x-m|表示数轴上的x对应点到1和m对应点的距离之和,其最小值为|m-1|,
若不等式|x-1|+|x-m|<2m的解集为∅,则有0<2m≤|m-1|,
故有
,解得 0<m<
,
故答案为 (0,
).
(2)曲线
(θ为参数)即 x2+(y-1)2=4,表示以C(0,1)为圆心,以2为半径的圆,
圆心到直线3x-4y-1=0的距离为d=
=1,故弦长为2
=2
=2
,
故答案为 2
.
(3)由于直角△ABC的内切圆与斜边AB相切于点D,且AD=1,BD=2,设内切圆半径为r,
则由勾股定理可得(1+r)2+(2+r)2=9,∴r2+3r=2.
△ABC的面积为
×(1+r)(2+r)=
(r2+3r+2)=2,
故答案为 2.
若不等式|x-1|+|x-m|<2m的解集为∅,则有0<2m≤|m-1|,
故有
|
| 1 |
| 3 |
故答案为 (0,
| 1 |
| 3 |
(2)曲线
|
圆心到直线3x-4y-1=0的距离为d=
| |0-4-1| |
| 5 |
| r2-d2 |
| 4-1 |
| 3 |
故答案为 2
| 3 |
(3)由于直角△ABC的内切圆与斜边AB相切于点D,且AD=1,BD=2,设内切圆半径为r,
则由勾股定理可得(1+r)2+(2+r)2=9,∴r2+3r=2.
△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
故答案为 2.
点评:本题主要考查绝对值不等式的解法,直线和圆相交的性质,圆的切线性质、圆的参数方程,以及三角形中的几何计算,属于中档题.

练习册系列答案
相关题目
 满足
满足 ,则
,则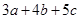 的最大值为_________.
的最大值为_________. 的直角边
的直角边 为直径的圆
为直径的圆 交
交 边于点
边于点 ,点
,点 在
在 上,且
上,且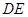 与圆
与圆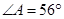 ,则
,则 _________.
_________. 与直线
与直线 的两个交点之间的距离为_________.
的两个交点之间的距离为_________. 满足
满足 ,则
,则 的最大值为_________.
的最大值为_________. 的直角边
的直角边 为直径的圆
为直径的圆 交
交 边于点
边于点 ,点
,点 在
在 上,且
上,且 与圆
与圆 ,则
,则 _________.
_________. 与直线
与直线 的两个交点之间的距离为_________.
的两个交点之间的距离为_________.