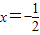题目内容
已知抛物线方程y2=mx(m∈R,且m≠0).(Ⅰ)若抛物线焦点坐标为(1,0),求抛物线的方程;
(Ⅱ)若动圆M过A(2,0),且圆心M在该抛物线上运动,E、F是圆M和y轴的交点,当m满足什么条件时,|EF|是定值.
分析:(Ⅰ)利用焦点坐标和抛物线系数间的关系即可求出抛物线的方程;
(Ⅱ)先把圆的方程用圆心坐标写出来,再让x=0求出关于,E、F的坐标和圆心坐标之间的关系式,把|EF|的长用圆心坐标和m表示出来.最后利用|EF|是定值求出m的值.
(Ⅱ)先把圆的方程用圆心坐标写出来,再让x=0求出关于,E、F的坐标和圆心坐标之间的关系式,把|EF|的长用圆心坐标和m表示出来.最后利用|EF|是定值求出m的值.
解答:解:(Ⅰ)依题意:
=1.(2分)
∴p=2∴所求方程为y2=4x.(4分)
(Ⅱ)设动圆圆心为M(a,b),(其中a≥0),E、F的坐标分别为(0,y1),(0,y2)
因为圆M过(2,0),
故设圆的方程(x-a)2+(y-b)2=(a-2)2+b2(6分)
∵E、F是圆M和y轴的交点
∴令x=0得:y2-2by+4a-4=0(8分)
则y1+y2=2b,y1•y2=4a-4
|EF|=
=
=
(10分)
又∵圆心M(a,b)在抛物线y2=mx上
∴b2=ma(11分)
∴|EF|=
=
.(12分)
∴当m=4时,|EF|=4(定值).(14分)
| p |
| 2 |
∴p=2∴所求方程为y2=4x.(4分)
(Ⅱ)设动圆圆心为M(a,b),(其中a≥0),E、F的坐标分别为(0,y1),(0,y2)
因为圆M过(2,0),
故设圆的方程(x-a)2+(y-b)2=(a-2)2+b2(6分)
∵E、F是圆M和y轴的交点
∴令x=0得:y2-2by+4a-4=0(8分)
则y1+y2=2b,y1•y2=4a-4
|EF|=
| (y1-y2)2 |
| (y1+y2)2-4y1•y2 |
| 4b2-16a+16 |
又∵圆心M(a,b)在抛物线y2=mx上
∴b2=ma(11分)
∴|EF|=
| 4ma-16a+16 |
| 4a(m-4)+16 |
∴当m=4时,|EF|=4(定值).(14分)
点评:一般在涉及到定值问题时,是让于变化量无关的项恒为0.比如本题是让m-4=0.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知抛物线方程y2=4x,过点P(1,2)的直线与抛物线只有一个交点,这样的直线有( )
| A、0条 | B、1条 | C、2条 | D、3条 |