题目内容
已知函数y=f(x)是定义在R上的增函数,函数y=f(x-1)的图像关于点(1,0)对称,若对任的x,y∈R,不等式f( -6x+21)+f(
-6x+21)+f(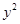 -8y)<0恒成立,则当x>3时,
-8y)<0恒成立,则当x>3时,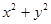 的取值范围是( )
的取值范围是( )
A (3,7) B (9,25) C (13,49) D (9,49)
C
解析考点:函数恒成立问题;函数单调性的性质;函数的图象.
专题:综合题.
分析:由函数y=f(x-1)的图象关于点(1,0)对称,结合图象平移的知识可知函数y=f(x)的图象关于点(0,0)对称,从而可知函数y=f(x)为奇函数,由f(x -6x+21)+f(y
-6x+21)+f(y -8y)<0恒成立,可把问题转化为(x-3)
-8y)<0恒成立,可把问题转化为(x-3) +(y-4)
+(y-4) <4,借助于的有关知识可求.
<4,借助于的有关知识可求.
解答: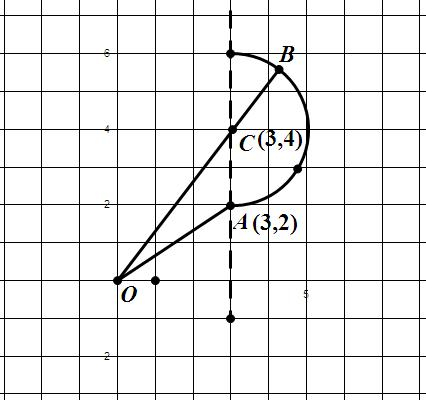
解:∵函数y=f(x-1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
即函数y=f(x)为奇函数,则f(-x)=-f(x),
又∵f(x)是定义在R上的增函数且f(x -6x+21)+f(y
-6x+21)+f(y -8y)<0恒成立
-8y)<0恒成立
∴f(x -6x+21)<-f(y
-6x+21)<-f(y -8y)=f(8y-y
-8y)=f(8y-y )恒成立,
)恒成立,
∴x -6x+21<8y-y
-6x+21<8y-y ,
,
∴(x-3) +(y-4)
+(y-4) <4恒成立,
<4恒成立,
设M (x,y),则当x>3时,M表示以(3,4)为圆心2为半径的右半圆内的任意一点,
则d= 表示区域内的点和原点的距离.
表示区域内的点和原点的距离.
由下图可知:d的最小值是OA=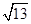 ,
,
OB=OC+CB,5+2=7,
当x>3时,x +y
+y 的范围为(13,49).
的范围为(13,49).
故答案为:(13,49).
点评:本题考查了函数图象的平移、函数的奇偶性、单调性及圆的有关知识,解决问题的关键是把“数”的问题转化为“形”的问题,借助于图形的几何意义减少了运算量,体现“数形结合:及”转化”的思想在解题中的应用.

 名校课堂系列答案
名校课堂系列答案已知函数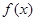 的图象如图,则
的图象如图,则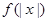 的图象为 ( )
的图象为 ( )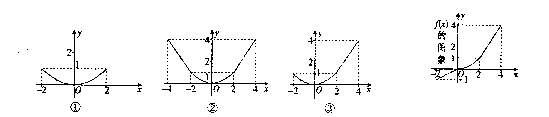
| A.① | B.② | C.③ | D.①②③图都不对 |
(文)函数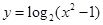 的定义域为 ( )
的定义域为 ( )
A.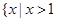 或 或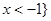 | B.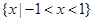 |
C.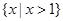 | D.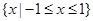 |
设 是
是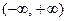 上的偶函数,
上的偶函数, . 当
. 当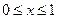 时有
时有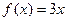 ,则
,则 等于
等于
A.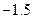 | B. | C.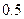 | D.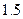 |
已知函数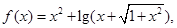 且
且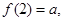 则
则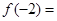 ( )
( )
A.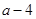 | B.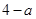 | C.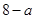 | D.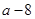 |
已知函数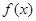 定义域为R,则
定义域为R,则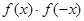 一定为 (
一定为 (
| A.偶函数 | B.奇函数 |
| C.非奇非偶函数 | D.既奇又偶函数 |
函数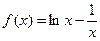 的零点所在的区间为( )
的零点所在的区间为( )
| A.(0,1 ) | B.(1,2) | C.(2,3) | D.(3,4) |
若x∈(e-1,1),a=ln x,b=2ln x,c=ln3x,则( )
| A.a<b<c | B.c<a<b |
| C.b<a<c | D.b<c<a |
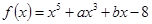 ,且
,且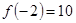 ,那么
,那么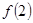 等于( )
等于( )