题目内容
设双曲线的左准线与两条渐近线交于A,B两点,左焦点为在以AB为直径的圆内,则该双曲线的离心率的取值范围为( )
A、(0,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(
|
分析:求出渐近线方程及准线方程;求得它们的交点A,B的坐标;利用圆内的点到圆心距离小于半径,列出参数a,b,c满足的不等式,求出离心率的范围.
解答:解:渐近线y=±
x.
准线x=±
,
求得A(-
,
).B(-
,-
),
左焦点为在以AB为直径的圆内,
得出 -
+c<
,
<
,
b<a,
c2<2a2
∴1<e<
,
故选B.
| b |
| a |
准线x=±
| a2 |
| c |
求得A(-
| a2 |
| c |
| ab |
| c |
| a2 |
| c |
| ab |
| c |
左焦点为在以AB为直径的圆内,
得出 -
| a2 |
| c |
| ab |
| c |
| b2 |
| c |
| ab |
| c |
b<a,
c2<2a2
∴1<e<
| 2 |
故选B.
点评:本题考查双曲线的准线、渐近线方程形式、考查园内的点满足的不等条件、注意双曲线离心率本身要大于1.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
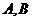 两点,左焦点为在以
两点,左焦点为在以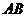 才为之直径的圆内,则该双曲线的离心率的取值范围为
才为之直径的圆内,则该双曲线的离心率的取值范围为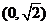 (B)
(B)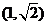 (C)
(C) 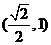 (D)
(D)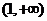
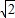 )
)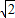 )
)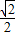 ,1)
,1)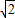 ,+∞)
,+∞)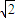 )
)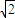 )
)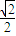 ,1)
,1)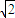 ,+∞)
,+∞)