题目内容
在平面直角坐标系 中,若圆
中,若圆 上存在
上存在 ,
, 两点关于点
两点关于点 成中心对称,则直线
成中心对称,则直线 的方程为
的方程为
x+y-3=0
解析试题分析:由题意,圆x2+(y-1)2=4的圆心坐标为C(0,1),
∵圆x2+(y-1)2=4上存在A,B两点关于点P(1,2)成中心对称,
∴CP⊥AB,P为AB的中点,
∵kCP=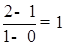 ,∴kAB=-1,
,∴kAB=-1,
∴直线AB的方程为y-2=-(x-1),即x+y-3=0.
故答案为:x+y-3=0..
考点:直线与圆的位置关系.

练习册系列答案
相关题目
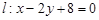 和两点
和两点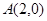 ,
,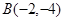 ,若直线
,若直线 上存在点
上存在点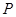 使得
使得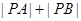 最小,则点
最小,则点 的倾斜角的大小是____________.
的倾斜角的大小是____________. 且垂直于直线
且垂直于直线 的直线
的直线 的方程为 .
的方程为 .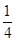 ,那么θ等于________.
,那么θ等于________. 的倾斜角的大小为 。
的倾斜角的大小为 。 ,m)共线,则实数m=________.
,m)共线,则实数m=________.